
【题目】如图,动点M在以O为圆心,AB为直径的半圆弧上运动(点M不与点A、B 及 ![]() 的中点F 重合),连接OM.过点M 作ME⊥AB于点E,以BE为边在半圆同侧作正方形BCDE,过点M作⊙O的切线交射线DC于点N,连接BM、BN.
的中点F 重合),连接OM.过点M 作ME⊥AB于点E,以BE为边在半圆同侧作正方形BCDE,过点M作⊙O的切线交射线DC于点N,连接BM、BN.
(1)探究:如图一,当动点M在 ![]() 上运动时;
上运动时;
①判断△OEM∽△MDN是否成立?请说明理由;
②设 ![]() =k,k是否为定值?若是,求出该定值,若不是,请说明理由;
=k,k是否为定值?若是,求出该定值,若不是,请说明理由;
③设∠MBN=α,α是否为定值?若是,求出该定值,若不是,请说明理由;
(2)拓展:如图二,当动点M 在 ![]() 上运动时;
上运动时;
分别判断(1)中的三个结论是否保持不变?如有变化,请直接写出正确的结论.(均不必说明理由)
【答案】
(1)
解:①△OEM∽△MDN成立,理由如下:
∵四边形BCDE是正方形,
∴BE=BC,∠EBC=∠CDE=∠BCD=∠BED=90°,
∴∠EOM+∠EMO=90°,
∵MN是⊙O的切线,
∴MN⊥OM,
∴∠OMN=90°,
∴∠DMN+∠EMO=90°,
∴∠EOM=∠DMN,
∴△OEM∽△MDN;
②k值为定值1;理由如下:
作BG⊥MN于G,如图一所示:
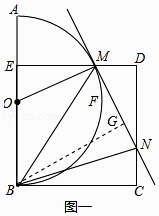
则BG∥OM,∠BGN=∠BGM=90°,
∴∠OMB=∠GBM,
∵OB=OM,
∴∠OBM=∠OMB,
∴∠OBM=∠GBM,
在△BME和△BMG中,  ,
,
∴△BME≌△BMG(AAS),
∴EM=GM,BE=BG,
∴BG=BC,
在Rt△BGN和Rt△BCN中, ![]() ,
,
∴Rt△BGN≌Rt△BCN(HL),
∴GN=CN,
∴EM+NC=GM+NC=MN,
∴k= ![]() =
= ![]() =1;
=1;
③设∠MBN=α,α为定值45°;理由如下:
∵△BME≌△BMG,Rt△BGN≌Rt△BCN,
∴∠EBM=∠GBM,∠GBN=∠CBN,
∴∠MBN= ![]() ∠EBC=45°,
∠EBC=45°,
即α=45°
(2)
解:(1)中的三个结论保持不变;理由同(1),
作BG⊥MN于G,如图二所示.

【解析】(1)①由正方形的性质得出BE=BC,∠EBC=∠CDE=∠BCD=∠BED=90°,由切线的性质和直角三角形的性质证出∠EOM=∠DMN,即可得出△OEM∽△MDN;②作BG⊥MN于G,则BG∥OM,∠BGN=∠BGM=90°,由平行线的性质和等腰三角形的性质得出∠OBM=∠GBM,由AAS证明△BME≌△BMG,得出EM=GM,BE=BG,证出BG=BC,由HL证明Rt△BGN≌Rt△BCN,得出GN=CN,证出EM+NC=GM+NC=MN,即可得出结论;③由全等三角形的性质得出∠EBM=∠GBM,∠GBN=∠CBN,求出∠MBN= ![]() ∠EBC=45°即可;(2)(1)中的三个结论保持不变;解法同(1).
∠EBC=45°即可;(2)(1)中的三个结论保持不变;解法同(1).


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC,∠C=90°,AC=3,BC=4.分别以点A、B为圆心画圆.如果点C在⊙A内,点B在⊙A外,且⊙B与⊙A内切,那么⊙B的半径长r的取值范围是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y= ![]() 的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3.
的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3. 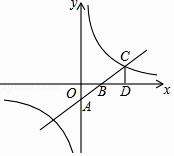
(1)求一次函数与反比例函数的解析式;
(2)直接写出当x>0时,kx+b﹣ ![]() <0的解集.
<0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:对角线互相垂直的平行四边形是菱形.
小红同学根据题意画出了图形,并写出了已知和求证的一部分,请你补全已知和求证,并写出证明过程.
①已知:如图,在ABCD中,对角线AC,BD交于点O,________.
②求证:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了备战初三物理、化学实验操作考试,某校对初三学生进行了模拟训练,物理、化学各有4各不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示,测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.
(1)请用树形图法或列表法,表示某个同学抽签的各种可能情况.
(2)小张同学对物理的①、②和化学的b、c号实验准备得较好,他同时抽到两科都准备的较好的实验题目的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读】
如图1,在平面直角坐标系xOy中,已知点A(a,0)(a>0),B(2,3),C(0,3).过原点O作直线l,使它经过第一、三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(1)【理解】
若点D与点A重合,则这个操作过程为FZ[ , ];
(2)【尝试】
若点D恰为AB的中点(如图2),求θ;
(3)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形0ABC的边AB上,求出a的值;若点E落在四边形0ABC的外部,直接写出a的取值范围;
(4)【探究】
经过FZ[θ,a]操作后,作直线CD交x轴于点G,交直线AB于点H,使得△ODG与△GAH是一对相似的等腰三角形,直接写出FZ[θ,a].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明为好友制作了一个如图所示的正方体礼品盒,在六个面上各有一字,连起来就是“祝取得好成绩”,其中“祝”的对面是“得”,“成”的对面是“绩”,则它的平面展开图可能是( )
A.
B.
C.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1= ![]() (x<0)图象上一点,AO的延长线交函数y2=
(x<0)图象上一点,AO的延长线交函数y2= ![]() (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC=
(x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC= ![]() ,求函数y2 .
,求函数y2 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com