
����Ŀ������ij��ѧΪ���˽⺢���Ƕԡ��й�ʫ�ʴ�ᡷ������ս�����ܡ�������ǿ���ԡ�����������˵�ҡ����������й������ֵ��ӽ�Ŀ��ϲ���̶ȣ�������ߡ��ˡ����꼶��ȡ�˲���ѧ�����е��飨ÿ��ֻ��ѡ��һ��ϲ���ĵ��ӽ�Ŀ����������õ����ݽ������������Ƴ�����������������ͳ��ͼ�����������ͳ��ͼ�е���Ϣ�ش��������⣺
��1�����ε����й���ȡ���� ����ѧ����
��2����ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У�ϲ���������й�����Ŀ���������ڵ����ε�Բ�Ľ����� ���ȣ�
��4������ѧУ��2000�ˣ�������Ƹ�ѧУϲ������ǿ���ԡ���Ŀ��ѧ�������Ƕ����ˣ�
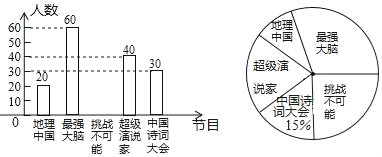
���𰸡���1��200����2����ͼ����������3��36����4��600��.
�������������������1����ϲ�����й�ʫ�ʴ�ᡷ������������ռ�İٷֱ���ʽ���㼴�ɣ�
��2�����ϲ������ս�����ܡ���Ŀ��������������ͳ��ͼ�����������ɣ�
��3����360���ϲ���������й�����Ŀ������ռ�������İٷ������ɵõ����ۣ�
��4��ֱ������������������ķ�����⼴����ô𰸣�
���������
�⣺��1��30��15%��200����
�𣺱��ε����й���ȡ��200��ѧ����
�ʴ�Ϊ��200��
��2��ϲ������ս�����ܡ���Ŀ��������200��20��60��40��30��50����
��ȫ����ͳ��ͼ��ͼ��ʾ��
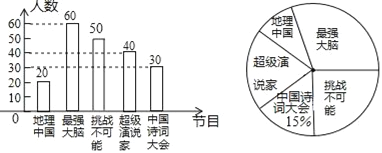
��3��ϲ���������й�����Ŀ���������ڵ����ε�Բ�Ľ���360���![]() ��36�ȣ�
��36�ȣ�
�ʴ�Ϊ��36��
��4��2000��![]() ��600����
��600����
�𣺸�ѧУϲ������ǿ���ԡ���Ŀ��ѧ��������600�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ף�AB��BD��CD��BD��AP��PC������ֱ�ΪB��P��D��������������ͬһֱ���ϣ����ǰ�������ͼ�νС�����ͼ����
��1��֤����ABCD=PBPD��
��2����ͼ�ң�Ҳ��һ��������ͼ�����������۳�������˵�����ɣ�
��3����֪��������x�ύ�ڵ�A��-1��0����B��3��0������y�ύ�ڵ㣨0��-3��������ΪP����ͼ����ʾ����Q��������������A��B��P�ĵ㣬ʹ�á�QAP=90������Q�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC����BAC��60�����ڡ�ABC�������ֱ��AP����C����ֱ��AP�ĶԳƵ�ΪD������AD��BD��
��1���������ⲹȫͼ�Σ�
��2������PAC���ڶ��ٶ�ʱ��AD��BC����˵�����ɣ�
��3����BD��ֱ��AP�ڵ�E������CE�����CED�Ķ�����
��4��̽�����߶�CE��AE��BE֮���������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶Ϊ�˽���÷�������������ȡ�˸��꼶����ѧ����������ij���ڿ����Ϸ��Դ���������ͳ�ƣ��������±�������������ͼ��ʾ��������������ͳ��ͼ����֪![]() ��
��![]() ���鷢�������ı�Ϊ
���鷢�������ı�Ϊ![]() ������ͼ���������Ϣ���ش��������⣺
������ͼ���������Ϣ���ش��������⣺
��� | ���Դ��� |
|
|
|
|
|
|
|
|
|
|
|
|

��1�������������������ȫ����ͳ��ͼ��
��2����![]() ���������ε�Բ�ĽǵĶ�����
���������ε�Բ�ĽǵĶ�����
��3�����꼶����ѧ��800�ˣ�������Ƹ��꼶��������Դ���������12������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC���������㶼�ڸ���ϣ���A������Ϊ��2��2�������������⣺
��1��������ABC����y��ԳƵ���A1B1C1����д��A1�����꣮
��2��������ABC�Ƶ�B��ʱ����ת90����õ�����A2B2C2����д��A2�����꣮
��3��������A2B2C2����ԭ��O�����ĶԳƵ���A3B3C3����д��A3�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ��չ�װ��ķ�ƶ����������60�ִ�������ƶ���������ƶ���������мס������ֻ����������ã���֪һ�����ֻ�����3�����ֻ���һ�ο�����29�ִ��ף�2�����ֻ�����3�����ֻ���һ�ο�����37�ִ��ף�
��1����ÿ�����ֻ�����ÿ�����ֻ���һ�ηֱ���װ�˶��ٶִ��ף�
��2����֪���ֻ���ÿ�����Ϊ500Ԫ�����ֻ���ÿ�����Ϊ450Ԫ������ҵ������8����������������û������ܷ���w��Ԫ�������ü��ֻ���������x������֮��ĺ�����ϵʽ��
��3���ڣ�2���������£�����Ϊ����ҵ��������������٣���������ٷ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����Ӳ����ʩ�������ɹ�80̨���ԣ�����A��B�����ͺŵĵ��Կɹ�ѡ����֪ÿ̨A�͵��Ա�B�͵Ĺ�2000Ԫ��2̨A�͵�����3̨B�͵��Թ���24000Ԫ��
��1���ֱ���A��B�����ͺŵ��Եĵ��ۣ�
��2����A��B�����ͺŵ��ԵIJɹ��ܼ۲�����38��Ԫ����A�͵������ɹ�����̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�У��Խ���BDƽ�֡�ABC����BAC=64�㣬��BCD+��DCA=180������ô��BDCΪ_________��.
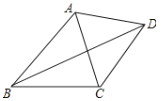
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪������y= ![]() ��x�ύ�ڵ�A����2��0���͵�B����y�ύ�ڵ�C��0����3����������A������AM��y���ཻ�ڵ�E���������ߵ���һ������ΪF����
��x�ύ�ڵ�A����2��0���͵�B����y�ύ�ڵ�C��0����3����������A������AM��y���ཻ�ڵ�E���������ߵ���һ������ΪF����![]() .
.
��1�������������ߵı���ʽ����д�����ĶԳ��
��2�����FAB������ֵ��
��3����D�ǵ�C���������߶Գ���ĶԳƵ㣬��P��y����һ�㣬�ҡ�AFP=��DAB�����P�����꣮
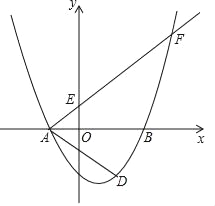
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com