
����Ŀ��ij��ҵ��չ�װ��ķ�ƶ����������60�ִ�������ƶ���������ƶ���������мס������ֻ����������ã���֪һ�����ֻ�����3�����ֻ���һ�ο�����29�ִ��ף�2�����ֻ�����3�����ֻ���һ�ο�����37�ִ��ף�
��1����ÿ�����ֻ�����ÿ�����ֻ���һ�ηֱ���װ�˶��ٶִ��ף�
��2����֪���ֻ���ÿ�����Ϊ500Ԫ�����ֻ���ÿ�����Ϊ450Ԫ������ҵ������8����������������û������ܷ���w��Ԫ�������ü��ֻ���������x������֮��ĺ�����ϵʽ��
��3���ڣ�2���������£�����Ϊ����ҵ��������������٣���������ٷ����Ƕ���Ԫ��
���𰸡���1���׳�װ8�֣��ҳ�װ7�֣���2��w=500x+450��8��x��=50x+3600��1��x��8����
��3������4���׳���4���ҳ�ʱ���˷���ʡ��Ϊ50��4+3600=3800Ԫ��
�������������������1�����������г���������⼴�ɣ�
��2���������ķ�����Ӽ�������ܷ��õĺ�������ʽ��
��3������һ�κ����õ���xԽСʱ���ܷ���ԽС���ֱ����1��2��3��4�õ���Сֵ���ɣ�
���������
�⣺��1������ֻ���x�������ֻ���y����
��������ã� ![]() ��
��
��ã� ![]() ��
��
�𣺼׳�װ8�֣��ҳ�װ7�֣�
��2����׳�x�������ҳ�Ϊ��8��x������
��������ã�w��500x��450��8��x����50x��3600��1��x��8����
��3���ߵ�x��1ʱ����8��x��7��8��7��7��57��60�֣��������⣻
��x��2ʱ����8��x��6��8��2��7��6��58��60�֣��������⣻
��x��3ʱ����8��x��5��8��3��7��5��59��60�֣��������⣻
��x��4ʱ����8��x��4��8��4��7��4��60�֣��������⣻
������4���׳���4���ҳ�ʱ���˷���ʡ��Ϊ50��4��3600��3800Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˹���о����н���������˿ͷ�һ���Թ�����![]() Ԫ���ɻ��һ��ҡ������.ҡ������һ��Բ��ת�̣����ȷֳ�
Ԫ���ɻ��һ��ҡ������.ҡ������һ��Բ��ת�̣����ȷֳ�![]() �����Σ����ת��ֹͣ��ָ�����ö���ƻ���ɫ���˿;Ϳ��Էֱ���һ���������Ƚ���������Ϊ
�����Σ����ת��ֹͣ��ָ�����ö���ƻ���ɫ���˿;Ϳ��Էֱ���һ���������Ƚ���������Ϊ![]() Ԫ��
Ԫ��![]() Ԫ��
Ԫ��![]() Ԫһ���Թ�����
Ԫһ���Թ�����![]() Ԫ�ߣ������ҡ���ɷ�������
Ԫ�ߣ������ҡ���ɷ�������![]() Ԫ.
Ԫ.

(1)ҡ��һ�Σ���һ�Ƚ������Ƚ������Ƚ��ĸ��ʷֱ��Ƕ��٣�
(2)С��һ���Թ�����![]() Ԫ���Dz���ҡ�����㣬������
Ԫ���Dz���ҡ�����㣬������![]() Ԫ�ֽ��㣿�����������
Ԫ�ֽ��㣿�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD��P�ǶԽ���AC������һ�㣬EΪAD�ϵĵ㣬�ҡ�EPB=90����PM��AD��PN��AB��
��1����֤���ı���PMAN�������Σ�
��2����֤��EM=BN��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
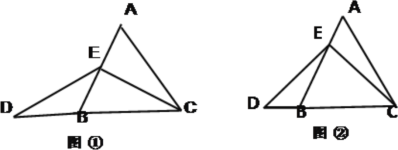
����Ŀ���ڵȱߡ�ABC�У���E��AB�ϣ���D��CB�ӳ����ϣ���ED=EC.
(1)����EΪAB�е�ʱ����ͼ�٣�AE DB���������������=��������˵������;
(2)����EΪAB������һ��ʱ����ͼ�ڣ�AE DB���������������=��������˵������;����ʾ������E��EF��BC����AC�ڵ�F��
(3)�ڵȱߡ�ABC�У���E��ֱ��AB�ϣ���D��ֱ��BC�ϣ���ED=EC.����ABC�ı߳�Ϊ1��AE=2�����㻭��ͼ�Σ���ֱ��д����Ӧ��CD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
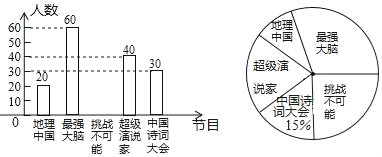
����Ŀ������ij��ѧΪ���˽⺢���Ƕԡ��й�ʫ�ʴ�ᡷ������ս�����ܡ�������ǿ���ԡ�����������˵�ҡ����������й������ֵ��ӽ�Ŀ��ϲ���̶ȣ�������ߡ��ˡ����꼶��ȡ�˲���ѧ�����е��飨ÿ��ֻ��ѡ��һ��ϲ���ĵ��ӽ�Ŀ����������õ����ݽ������������Ƴ�����������������ͳ��ͼ�����������ͳ��ͼ�е���Ϣ�ش��������⣺
��1�����ε����й���ȡ���� ����ѧ����
��2����ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У�ϲ���������й�����Ŀ���������ڵ����ε�Բ�Ľ����� ���ȣ�
��4������ѧУ��2000�ˣ�������Ƹ�ѧУϲ������ǿ���ԡ���Ŀ��ѧ�������Ƕ����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��y=��x+b�������ύ��C��D���㣬ֱ��AB�������ύ��A��B���㣬�߶�OA��OC�ij��Ƿ���x2��3x+2=0����������OA��OC����
��1�����A��C�����ꣻ
��2��ֱ��AB��ֱ��CD���ڵ�E������E���߶�AB���е㣬����������y=![]() ��k��0����ͼ���һ����֧������E����k��ֵ��
��k��0����ͼ���һ����֧������E����k��ֵ��
��3���ڣ�2���������£���M��ֱ��CD�ϣ�����ƽ�����Ƿ���ڵ�N��ʹ�Ե�B��E��M��NΪ������ı��������Σ������ڣ���ֱ��д�����������ĵ�N�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����C�ǡ�O�ϵ�һ�㣬DA���O�����ڵ�A��DA=DC=![]() ��
��

��1����֤��DC�ǡ�O�����ߣ�
��2������CAB=30�㣬����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
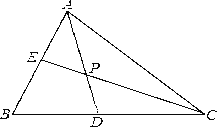
����Ŀ����ͼ����ABC�У���ABC��60�㣬AD��CE�ֱ�ƽ�֡�BAC����ACB��AD��CE�ཻ�ڵ�P
(1) ���CPD�Ķ���
(2) ��AE��3��CD��7�����߶�AC�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
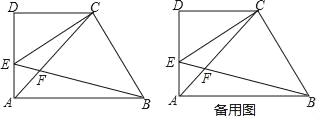
����Ŀ����֪����ͼ��������ABCD�У�AB��CD����D=90�㣬AD=CD=2����E�ڱ�AD�ϣ������A��D�غϣ�����CEB=45�㣬EB��Խ���AC�ཻ�ڵ�F����DE=x��
��1���ú�x�Ĵ���ʽ��ʾ�߶�CF�ij���
��2���������CAE���ܳ�����C��CAE����BAF���ܳ�����C��BAF����![]() =y����y����x�ĺ�����ϵʽ����д�����Ķ�����
=y����y����x�ĺ�����ϵʽ����д�����Ķ�����
��3������ABE������ֵ��![]() ʱ����AB�ij���
ʱ����AB�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com