
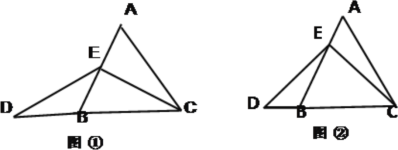
【题目】在等边△ABC中,点E在AB上,点D在CB延长线上,且ED=EC.
(1)当点E为AB中点时,如图①,AE DB(填“﹥”“﹤”或“=”),并说明理由;
(2)当点E为AB上任意一点时,如图②,AE DB(填“﹥”“﹤”或“=”),并说明理由;(提示:过点E作EF∥BC,交AC于点F)
(3)在等边△ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,请你画出图形,并直接写出相应的CD的长.
【答案】(1)=,理由见解析;(2)=,理由见解析;(3)见解析
【解析】
(1)根据等边三角形性质和等腰三角形的性质求出∠D=∠ECB=30°,求出∠DEB=30°,求出BD=BE即可;
(2)过E作EF∥BC交AC于F,求出等边三角形AEF,证△DEB和△ECF全等,求出BD=EF即可;
(3)当D在CB的延长线上,E在AB的延长线式时,由(2)求出CD=3,当E在BA的延长线上,D在BC的延长线上时,求出CD=1.
解:(1)=,理由如下:
∵ED=EC
∴∠D=∠ECD
∵△ABC是等边三角形
∴∠ACB=∠ABC=60°
∵点E为AB中点
∴∠BCE=∠ACE=30°,AE=BE
∴∠D=30°
∴∠DEB=∠ABC-∠D= 30°
∴∠DEB=∠D
∴BD=BE
∴BD=AE
(2) 过点E作EF∥BC,交AC于点F
∵△ABC是等边三角形
∴∠AEF=∠ABC=60°, ∠AFE=∠ACB=60°, ∠FEC=∠ECB
∴∠EFC=∠EBD=120°
∵ED=EC
∴∠D=∠ECD
∴∠D=∠FEC
在△EFC和 △DBE中

∴△EFC≌△DBE
∴EF=DB
∵∠AEF=∠AFE=60°
∴△AEF 为等边三角形
∴ AE=EF
∴DB =AE
(3)解:CD=1或3,
理由是:分为两种情况:
①如图3,过A作AM⊥BC于M,过E作EN⊥BC于N,

则AM∥EN,
∵△ABC是等边三角形,
∴AB=BC=AC=1,
∵AM⊥BC,
∴BM=CM=![]() BC=
BC=![]() ,
,
∵DE=CE,EN⊥BC,
∴CD=2CN,
∵AM∥EN,
∴△AMB∽△ENB,
∴![]() ,
,
∴![]() ,
,
∴BN=![]() ,
,
∴CN=1+![]() =
=![]() ,
,
∴CD=2CN=3;
②如图4,作AM⊥BC于M,过E作EN⊥BC于N,

则AM∥EN,
∵△ABC是等边三角形,
∴AB=BC=AC=1,
∵AM⊥BC,
∴BM=CM=![]() BC=
BC=![]() ,
,
∵DE=CE,EN⊥BC,
∴CD=2CN,
∵AM∥EN,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴MN=1,
∴CN=1-![]() =
=![]() ,
,
∴CD=2CN=1,
即CD=3或1.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距离O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,
(1)A处是否会受到火车的影响,并写出理由
(2)如果A处受噪音影响,求影响的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC(如图).
(1)利用尺规按下列要求作图(保留作图痕迹,不写作法):
①作∠BAC的平分线AD,交BC于点D;
②作AB边的垂直平分线EF,分别交AD,AB于点E,F.
(2)连接BE,若∠ABC=60°,∠C=40°,求∠AEB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,且经过点
,且经过点![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.

(1)求![]() 的值;
的值;
(2)求直线![]() 的解析式;
的解析式;
(3)根据图象,直接写出![]() 的解集.
的解集.
(4)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级为了解课堂发言情况,随机抽取了该年级部分学生,对他们某天在课堂上发言次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知![]() 、
、![]() 两组发言人数的比为
两组发言人数的比为![]() ,请结合图表中相关信息,回答下列问题:
,请结合图表中相关信息,回答下列问题:
组别 | 发言次数 |
|
|
|
|
|
|
|
|
|
|
|
|

(1)求出样本容量,并补全条形统计图;
(2)求![]() 组所在扇形的圆心角的度数;
组所在扇形的圆心角的度数;
(3)该年级共有学生800人,请你估计该年级在这天里发言次数不少于12的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板ABC和三角板BDE(∠ACB=∠DBE=90°,∠ABC=60°)按不同的位置摆放.
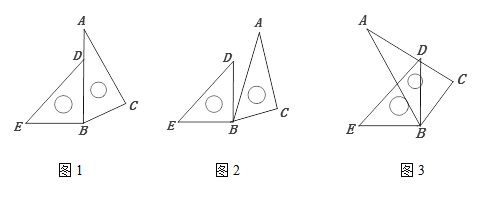
(1)如图1,若边BD,BA在同一直线上,则∠EBC= ;
(2)如图2,若∠EBC=165°,那么∠ABD= ;
(3)如图3,若∠EBC=120°,求∠ABD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业开展献爱心扶贫活动,将购买的60吨大米运往贫困地区帮扶贫困居民,现有甲、乙两种货车可以租用.已知一辆甲种货车和3辆乙种货车一次可运送29吨大米,2辆甲种货车和3辆乙种货车一次可运送37吨大米.
(1)求每辆甲种货车和每辆乙种货车一次分别能装运多少吨大米?
(2)已知甲种货车每辆租金为500元,乙种货车每辆租金为450元,该企业共租用8辆货车.请求出租用货车的总费用w(元)与租用甲种货车的数量x(辆)之间的函数关系式.
(3)在(2)的条件下,请你为该企业设计如何租车费用最少?并求出最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某相宜本草护肤品专柜计划在春节前夕促销甲、乙两款护肤品,根据市场调研,发现如下两种信息:
信息一:销售甲款护肤品所获利润y(元)与销售量x(件)之间存在二次函数关系y=ax2+bx.在x=10时,y=140;当x=30时,y=360.
信息二:销售乙款护肤品所获利润y(元)与销售量x(件)之间存在正比例函数关系y=3x.请根据以上信息,解答下列问题;
(1)求信息一中二次函数的表达式;
(2)该相宜本草护肤品专柜计划在春节前夕促销甲、乙两款护肤品共100件,请设计一个营销方案,使销售甲、乙两款护肤品获得的利润之和最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
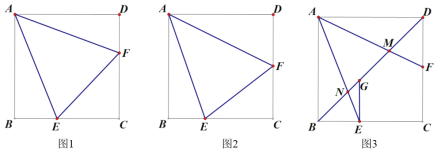
【题目】已知正方形 ABCD,E 在线段 BC 上,F 在线段 CD 上.
(1)如图 1,连接 EF,若EAF =45,求证:BE+DF=EF;
(2)如图 2,连接 EF,若DAE=AEF ,且 2BE=CE,求![]() 的值;
的值;
(3)如图 3,连接 BD,线段 AE、AF 分别交 BD 于点 N、M.已知GEB=90 ,DM=MG=4,NG=1,请直接写出线段AF 的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com