
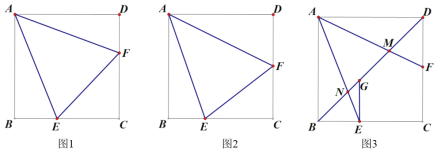
【题目】已知正方形 ABCD,E 在线段 BC 上,F 在线段 CD 上.
(1)如图 1,连接 EF,若EAF =45,求证:BE+DF=EF;
(2)如图 2,连接 EF,若DAE=AEF ,且 2BE=CE,求![]() 的值;
的值;
(3)如图 3,连接 BD,线段 AE、AF 分别交 BD 于点 N、M.已知GEB=90 ,DM=MG=4,NG=1,请直接写出线段AF 的长度.
【答案】(1)证明详见解析;(2)1;(3)![]()
【解析】
(1)如图,延长CB至M,使BM=DF,连接AM,证明△ABM≌△ADF,则AF=AM,进而可证明△AEF≌△AEM,可得ME=EF ,进而可得BE+DF=EF;
(2)如图,延长AD,EF交于点M。过M作MN⊥BC交BC的延长线于N,设BE=x,DM=y,则根据已知条件和正方形的性质,可求![]() ,
,![]() ,
,![]() ,
,![]() ,再根据勾股定理在Rt△ENM中可计算出
,再根据勾股定理在Rt△ENM中可计算出![]() ,再证△DMF∽△CEF,根据相似比即可求得
,再证△DMF∽△CEF,根据相似比即可求得![]() 的值;
的值;
(3)设![]() ,易证△GNE∽△BNA,根据相似比可求得
,易证△GNE∽△BNA,根据相似比可求得![]() ,再由△AMF∽△BMA,可得
,再由△AMF∽△BMA,可得![]() ,即可得
,即可得![]() ,再在Rt△ADF中,由勾股定理即可求得
,再在Rt△ADF中,由勾股定理即可求得![]() 的长.
的长.
解:(1)如图,延长CB至M,使BM=DF,连接AM,

∵四边形ABCD为正方形,
∴∠ABM=∠ADF=90°,AD=AB,
∴△ABM≌△ADF,
∴AF=AM,
∵∠EAF=45°,
∴![]() ,
,
∵![]() ,
,
∴△AEF≌△AEM,
∴ME=EF,
∴![]() ,
,
即BE+DF=EF得证;
(2)如图,延长AD,EF交于点M。过M作MN⊥BC交BC的延长线于N,

设BE=x,DM=y,
∴![]() ,
,![]() ,
,![]() ,
,
∵DAE=AEF
∴![]() ,
,
在Rt△ENM中,由勾股定理可得:![]() ,
,
解得:![]() ,
,
又∵AM∥BN,
∴∠DMF=∠FEC,
∵∠MDF=∠CEF=90°,
∴△DMF∽△CEF,
∴![]() ,
,
即![]() ;
;
(3)设![]() ,
,
∵GEB=90,
∴GE⊥AB,且∠ABG=∠EBG=45°,
易证△GNE∽△BNA,
∴ ,
,
即,![]() ,
,
解得:![]() ,
,
∴![]() ,
,![]() ,
,
又∵AB∥DC,
∴△DMF∽△BMA,
∴![]() ,
,
∴![]() ,
,
∴在Rt△ADF中,![]() ,
,
故![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
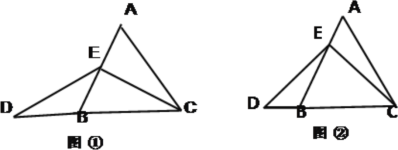
【题目】在等边△ABC中,点E在AB上,点D在CB延长线上,且ED=EC.
(1)当点E为AB中点时,如图①,AE DB(填“﹥”“﹤”或“=”),并说明理由;
(2)当点E为AB上任意一点时,如图②,AE DB(填“﹥”“﹤”或“=”),并说明理由;(提示:过点E作EF∥BC,交AC于点F)
(3)在等边△ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,请你画出图形,并直接写出相应的CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
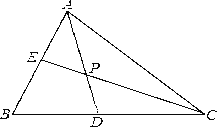
【题目】如图,△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,AD、CE相交于点P
(1) 求∠CPD的度数
(2) 若AE=3,CD=7,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“五·一车展”期间,某汽车经销商推出![]() 四种型号的轿车共1000辆进行展销,
四种型号的轿车共1000辆进行展销,![]() 型号轿车销售的成交率(售出数量
型号轿车销售的成交率(售出数量![]() 展销数量)为50%,图1是各型号参展轿车的百分比,图2是已售出的各型号轿车的数量,(两幅统计图尚不完整)
展销数量)为50%,图1是各型号参展轿车的百分比,图2是已售出的各型号轿车的数量,(两幅统计图尚不完整)

(1)参加展销的![]() 型号轿车有多少辆?
型号轿车有多少辆?
(2)请你将图2的统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了推动球类运动的普及,成立多个球类运动社团,为此,学生会采取抽样调查的方法,从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好(要求每位同学只能选择其中一种自己喜欢的球类运动),并将调查结果绘制成了如下条形统计图和扇形统计图(不完整).请你根据图中提供的信息,解答下列问题:

(1)本次抽样调查,共调查了 名学生;
(2)请将条形统计图和扇形统计图补充完整;
(3)若该学校共有学生1800人,根据以上数据分析,试估计选择排球运动的同学约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,现同时将点
,现同时将点![]() ,
,![]() 分别向上平移
分别向上平移![]() 个单位,再向右平移
个单位,再向右平移![]() 个单位,分别得到点
个单位,分别得到点![]() ,
,![]() 的对应点
的对应点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .(三角形可用符号
.(三角形可用符号![]() 表示,面积用符号
表示,面积用符号![]() 表示)
表示)

(1)直接写出点![]() ,
,![]() 的坐标.
的坐标.
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,连接
,连接![]() ,
,![]() ,使
,使![]() ,若存在,请求出点
,若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)点![]() 在直线
在直线![]() 上运动,连接
上运动,连接![]() ,
,![]() .
.
①若![]() 在线段
在线段![]() 之间时(不与
之间时(不与![]() ,
,![]() 重合),求
重合),求![]() 的取值范围;
的取值范围;
②若![]() 在直线
在直线![]() 上运动,请直接写出
上运动,请直接写出![]() ,
,![]() ,
,![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
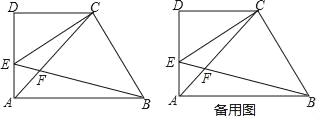
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的“学习强国”阅读知识竞赛中,有901班和902班两个班参加比赛且人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分和70分.年级组长李老师将901班和902班的成绩进行整理并绘制成如下的统计图:
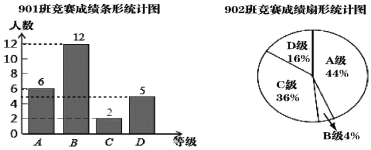
平均数(分) | 中位数(分) | 众数(分) | B级及以上人数 | |
901班 | 87.6 | 90 | 18 | |
902班 | 87.6 | 100 |
(1)在本次竞赛中,902班C级及以上的人数有多少?
(2)请你将表格补充完整:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com