
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,现同时将点
,现同时将点![]() ,
,![]() 分别向上平移
分别向上平移![]() 个单位,再向右平移
个单位,再向右平移![]() 个单位,分别得到点
个单位,分别得到点![]() ,
,![]() 的对应点
的对应点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .(三角形可用符号
.(三角形可用符号![]() 表示,面积用符号
表示,面积用符号![]() 表示)
表示)

(1)直接写出点![]() ,
,![]() 的坐标.
的坐标.
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,连接
,连接![]() ,
,![]() ,使
,使![]() ,若存在,请求出点
,若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)点![]() 在直线
在直线![]() 上运动,连接
上运动,连接![]() ,
,![]() .
.
①若![]() 在线段
在线段![]() 之间时(不与
之间时(不与![]() ,
,![]() 重合),求
重合),求![]() 的取值范围;
的取值范围;
②若![]() 在直线
在直线![]() 上运动,请直接写出
上运动,请直接写出![]() ,
,![]() ,
,![]() 的数量关系.
的数量关系.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】将一副三角板ABC和三角板BDE(∠ACB=∠DBE=90°,∠ABC=60°)按不同的位置摆放.
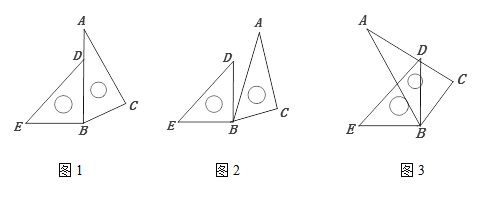
(1)如图1,若边BD,BA在同一直线上,则∠EBC= ;
(2)如图2,若∠EBC=165°,那么∠ABD= ;
(3)如图3,若∠EBC=120°,求∠ABD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
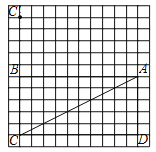
【题目】如图,12×12的正方形网格中的每个小正方形的边长都是1,正方形的顶点叫做格点.矩形ABCD的四个顶点A,B,C,D都在格点上,将△ADC绕点A顺时针方向旋转得到△AD′C′,点C与点C′为对应点.
(1)在正方形网格中确定D′的位置,并画出△AD′C′;
(2)若边AB交边C′D′于点E,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中的每一个小方格都是是边长为 1 个单位的正方形,只能使用无刻度直尺,请以格点为顶点按照以下要求作图:
(1)请在图 1 中画出ABC,其中AC=![]() ,AB=
,AB=![]() ,BC=
,BC=![]() ;
;
(2)请在图 2 中画出面积为 8 的正方形 ABCD,且找出点 O,使得经过点 O 的所有直线都平分正方形ABCD 的面积,保留作图痕迹.

查看答案和解析>>
科目:初中数学 来源: 题型:
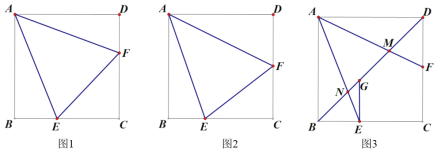
【题目】已知正方形 ABCD,E 在线段 BC 上,F 在线段 CD 上.
(1)如图 1,连接 EF,若EAF =45,求证:BE+DF=EF;
(2)如图 2,连接 EF,若DAE=AEF ,且 2BE=CE,求![]() 的值;
的值;
(3)如图 3,连接 BD,线段 AE、AF 分别交 BD 于点 N、M.已知GEB=90 ,DM=MG=4,NG=1,请直接写出线段AF 的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎使得湖北的物资紧缺,为支援疫区,某村捐赠蔬菜30吨,水果13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往港口,已知一辆甲种货车可装蔬菜和水果共5吨,且一辆甲种货车可装的蔬菜重量(单位:吨)是其可装的水果重量的4倍,一辆乙种货车可装蔬菜水果各2吨;
(1)一辆甲种货车可装载蔬菜、水果各多少吨?
(2)该村安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1500元,则该村应选择哪种方案?使运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
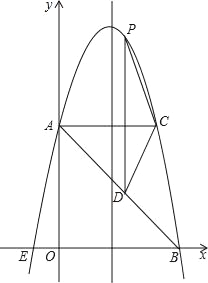
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.
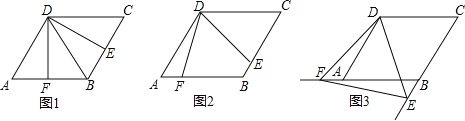
(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由;
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com