
【题目】新冠肺炎使得湖北的物资紧缺,为支援疫区,某村捐赠蔬菜30吨,水果13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往港口,已知一辆甲种货车可装蔬菜和水果共5吨,且一辆甲种货车可装的蔬菜重量(单位:吨)是其可装的水果重量的4倍,一辆乙种货车可装蔬菜水果各2吨;
(1)一辆甲种货车可装载蔬菜、水果各多少吨?
(2)该村安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1500元,则该村应选择哪种方案?使运费最少?最少运费是多少元?
【答案】(1)4;1 (2)三种方案:甲5辆,乙5辆;甲6辆,乙4辆;甲7辆,乙3辆 (3)方案1;17500元
【解析】
(1)设一辆甲种货车可装载蔬菜x吨,水果y吨,根据“一辆甲种货车可装蔬菜和水果共5吨,且一辆甲种货车可装的蔬菜重量是其可装的水果重量的4倍”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设安排m辆甲种货车,则安排(10-m)辆乙种货车,根据这10辆车可一次将30吨蔬菜和13吨水果运完,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,再结合m为整数,即可得出各运货方案;
(3)根据总运费=单辆车的运费×所用该种车型的辆数,即可分别求出三种运货方案所需总运费,比较后即可得出结论.
解:(1)设一辆甲种货车可装载蔬菜x吨,水果y吨, 依题意,得:
![]() ,
,
解得:![]() .
.
答:一辆甲种货车可装载蔬菜4吨,水果1吨.
(2)设安排m辆甲种货车,则安排(10-m)辆乙种货车, 依题意,得:
![]()
解得:5≤m≤7.
∵m为整数,
∴m=5,6,7,
∴共有三种方案,
方案1:安排5辆甲种货车,5辆乙种货车;
方案2:安排6辆甲种货车,4辆乙种货车;
方案3:安排7辆甲种货车,3辆乙种货车.
(3)方案1所需费用2000×5+1500×5=17500(元);
方案2所需费用2000×6+1500×4=18000(元);
方案3所需费用2000×7+1500×3=18500(元).
∵17500<18000<18500,
∴该果农应选方案1,使运费最少,最少运费是17500元.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程x2﹣3x+2=0的两个根(OA>OC).
(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数y=![]() (k≠0)的图象的一个分支经过点E,求k的值;
(k≠0)的图象的一个分支经过点E,求k的值;
(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“五·一车展”期间,某汽车经销商推出![]() 四种型号的轿车共1000辆进行展销,
四种型号的轿车共1000辆进行展销,![]() 型号轿车销售的成交率(售出数量
型号轿车销售的成交率(售出数量![]() 展销数量)为50%,图1是各型号参展轿车的百分比,图2是已售出的各型号轿车的数量,(两幅统计图尚不完整)
展销数量)为50%,图1是各型号参展轿车的百分比,图2是已售出的各型号轿车的数量,(两幅统计图尚不完整)

(1)参加展销的![]() 型号轿车有多少辆?
型号轿车有多少辆?
(2)请你将图2的统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,现同时将点
,现同时将点![]() ,
,![]() 分别向上平移
分别向上平移![]() 个单位,再向右平移
个单位,再向右平移![]() 个单位,分别得到点
个单位,分别得到点![]() ,
,![]() 的对应点
的对应点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .(三角形可用符号
.(三角形可用符号![]() 表示,面积用符号
表示,面积用符号![]() 表示)
表示)

(1)直接写出点![]() ,
,![]() 的坐标.
的坐标.
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,连接
,连接![]() ,
,![]() ,使
,使![]() ,若存在,请求出点
,若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)点![]() 在直线
在直线![]() 上运动,连接
上运动,连接![]() ,
,![]() .
.
①若![]() 在线段
在线段![]() 之间时(不与
之间时(不与![]() ,
,![]() 重合),求
重合),求![]() 的取值范围;
的取值范围;
②若![]() 在直线
在直线![]() 上运动,请直接写出
上运动,请直接写出![]() ,
,![]() ,
,![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
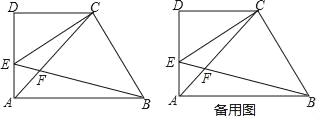
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() .点C在点
.点C在点![]() 的右侧,
的右侧,![]() ,
,![]() 平分么
平分么![]() ,平分
,平分![]() 所在的直线交于点
所在的直线交于点![]() ,点
,点![]() 在
在![]() 之间。
之间。
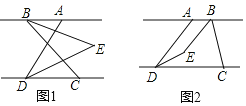
(1)如图1,点![]() 在点A的左侧,若
在点A的左侧,若![]() ,求
,求![]() 的度数?
的度数?
(2)如图2,点![]() 在点A的右侧,若
在点A的右侧,若![]() ,直接写出
,直接写出![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的“学习强国”阅读知识竞赛中,有901班和902班两个班参加比赛且人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分和70分.年级组长李老师将901班和902班的成绩进行整理并绘制成如下的统计图:
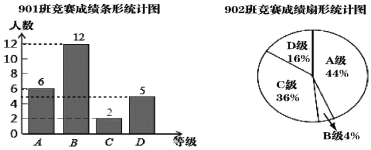
平均数(分) | 中位数(分) | 众数(分) | B级及以上人数 | |
901班 | 87.6 | 90 | 18 | |
902班 | 87.6 | 100 |
(1)在本次竞赛中,902班C级及以上的人数有多少?
(2)请你将表格补充完整:
查看答案和解析>>
科目:初中数学 来源: 题型:
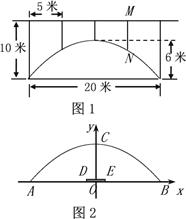
【题目】一座拱桥的截面轮廓为抛物线型(如图1),拱高6米,跨度20米,相邻两支柱间的距离均为5米.
(1)将抛物线放在所给的直角坐标系中(如图2所示),其表达式是![]() 的形式. 请根据所给的数据求出
的形式. 请根据所给的数据求出![]() 的值.
的值.
(2)求支柱MN的长度.
(3)拱桥下地平面是双向行车道(正中间DE是一条宽2米的隔离带),其中的一条行车道能否并排行驶宽2米、高3米的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小李8时骑自行车从家里出发,到野外郊游,16时回到家里.他离家的距离s(千米)与时间t(时)之间的函数关系可以用图中的折线表示.现有如下信息:
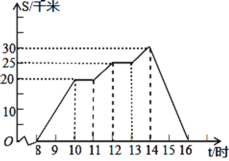
(1)小李到达离家最远的地方的时间是14时;
(2)小李第一次休息时间是10时;
(3)11时到12时,小李骑了5千米;
(4)返回时,小李的平均车速是10千米/时.
其中,正确的信息有___________________(填番号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com