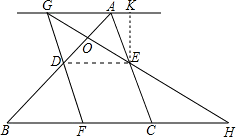
解:(1)如图,∵GA∥BC
∴

又∵AB=6,AD=2
∴DB=4
∵BF=t
∴
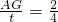
∴AG=

t
过点E作EK⊥AG,垂足为K,
∵∠BCA=60°,
∴∠CAK=60°,
∴∠AEK=30°,
∵AE=2,
∴AK=1,根据勾股定理得:EK=

,
∴S=

AG•EK=

×

t×

=

t;
(2)如图,连接DE,由AD=AE可知,△ADE为等边三角形.
∵AB⊥HG,
根据等腰三角形的三线合一可知:AO=OD,∠AEO=∠DEO,
∵GA∥DE,
∴∠AGE=∠OED,
∴∠AGE=∠AEO,
∴AG=AE=2,
∴

t=2,
∴t=4,
即当t=4时,AB⊥HG;
(3)∵GA∥BC,
∴
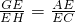
,
∴

,
∵DE∥BC,
∴

,
∴FH=BC,
∵△ABC与△GFH的高相等,
∴S
△GFH=S
△ABC=

×6×3

=9

,
∴不论t为何值,△GFH的面积均为9

;
分析:(1)在三角形EGA中,底边AG的长可通过相似三角形ADG和BDF利用相似三角形的对应边成比例求出,而AG边上的高可用AE•sin60°来表示,然后利用三角形的面积公式即可得出S、t的函数关系式;
(2)当AB⊥GE时,连接DE,由已知推出三角形ADE是等边三角形,可得∠AEG=60°,即∠AEG=∠DEO=30°,然后根据AG与DE的平行得出内错角的相等求出∠AGE=30°,进而根据等角对等边可得出AG=AE=2,在(1)中已经求出了AG的表达式),根据得出的等量关系即可求出t的值;
(3)由GA∥BC,DE∥BC,分别得出比例,经过转化可得出FH=BC,又由图观察可知△ABC与△GFH的高相等,所以
△ABC与△GFH的面积相等,求出等边三角形ABC的面积即为三角形GFH的面积,所以△GFH的面积为定值.
点评:本题主要考查了学生掌握相似三角形的性质与判断,同时要求学生掌握等边三角形的有关性质,会利用等边三角形中特殊角来求值,本题要求学生必须掌握求定值的方法,锻炼了学生的逻辑思维能力,提高了学生结合条件寻求结论解决数学问题的能力.

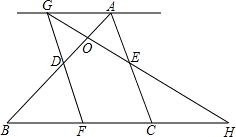 GE交AD于点O,并延长交BC延长线于点H.
GE交AD于点O,并延长交BC延长线于点H. 解:(1)如图,∵GA∥BC
解:(1)如图,∵GA∥BC
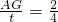
 t
t ,
, AG•EK=
AG•EK= ×
× t×
t× =
= t;
t; t=2,
t=2,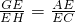 ,
, ,
, ,
, ×6×3
×6×3  =9
=9  ,
, ;
;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N. 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.