
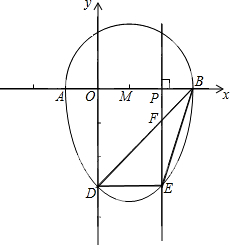
 ���ǰ�һ����Բ�������ߵ�һ���ֺϳɵķ��ͼ�γ�Ϊ����Բ�������һ��ֱ���롰��Բ��ֻ��һ�����㣬��ô����ֱ�߽�������Բ�������ߣ���ͼ����A��B��C��D�ֱ��ǡ���Բ����������Ľ��㣬��֪��D������Ϊ��0��-3����ABΪ��Բ��ֱ������ԲԲ��M������Ϊ��1��0������Բ�뾶Ϊ2��
���ǰ�һ����Բ�������ߵ�һ���ֺϳɵķ��ͼ�γ�Ϊ����Բ�������һ��ֱ���롰��Բ��ֻ��һ�����㣬��ô����ֱ�߽�������Բ�������ߣ���ͼ����A��B��C��D�ֱ��ǡ���Բ����������Ľ��㣬��֪��D������Ϊ��0��-3����ABΪ��Բ��ֱ������ԲԲ��M������Ϊ��1��0������Բ�뾶Ϊ2������ ��1�����ý���ʽ����֪����������������ʽ���ɣ�
��2���������C�����꣬�����ó�G�����꣬�����ó�ֱ��CG�Ľ���ʽ��
��3������S��BDE=S��DEF+S��BEF����ʾ��|EF|�ij��������ó����κ�����ֵ������ɣ�
��� �⣺��1�������A��-1��0����B��3��0����
��������Ϊy=a��x+1����x-3����
�������߹�D��0��-3����
��-3=a��0+1����0-3����
���a=1��y=��x+1����x-3����
��y=x2-2x-3��-1��x��3����
��2����ͼ������CM����C������Բ�����߽�x����G
��Rt��COM����OM=1��CM=2��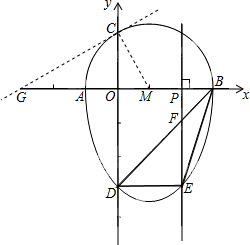
���OCM=30�㣬��CMO=60�㣬
��CO=$\sqrt{3}$����C��0��$\sqrt{3}$����
�֡�CG�С���Բ����C��
���GCM=90�㣬
���G=30�㣬
��Rt��GMC��GM=2CM=4��
��G��-3��0����
��ֱ��CG�Ľ���ʽΪy=kx+b��
��ֱ��CG����C��G���㣬
��$\left\{\begin{array}{l}\sqrt{3}=b\\ 0=-3k+b\end{array}\right.$��
��ã�$\left\{\begin{array}{l}k=\frac{{\sqrt{3}}}{3}\\ b=\sqrt{3}\end{array}\right.$��
��ֱ��CG�Ľ���ʽΪ$y=\frac{{\sqrt{3}}}{3}x+\sqrt{3}$��
��3�����ڵ�E������Ϊ$��\frac{3}{2}��-\frac{15}{4}��$��
��B��3��0����D��0��-3���ɵ�ֱ��BD�Ľ���ʽΪy=x-3
��P��m��0����F��m��m-3����E��m��m2-2m-3����
S��BDE=S��DEF+S��BEF
=$\frac{1}{2}��|EF|��m+\frac{1}{2}��|EF|����3-m��$
=$\frac{1}{2}��|EF|��3$��
|EF|=m-3-��m2-2m-3��=-m2-3m=-��m-$\frac{3}{2}$��2+$\frac{9}{4}$��
S��BDE=$\frac{1}{2}$[-��m-$\frac{3}{2}$��2+$\frac{9}{4}$]��3=$-\frac{3}{2}{��m-\frac{3}{2}��^2}+\frac{27}{8}$��
��0��m��3��
�൱$m=\frac{3}{2}$ʱ��BDE��������������Ϊ$\frac{27}{8}$��
��ʱE������Ϊ��$\frac{3}{2}$��$-\frac{15}{4}$����
���� ������Ҫ�����˶��κ����ۺ��Լ�����ʽ����κ�������ʽ�Լ�����ϵ������һ�κ�������ʽ��֪ʶ����ʾ��EF�ij��ǽ���ؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 1 | C�� | 0 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
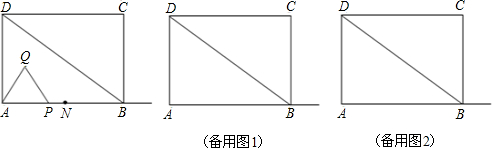
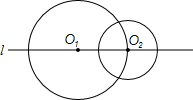 ��ͼ���뾶Ϊ4�ġ�O1��Բ��O1��ֱ��l�ϣ��뾶Ϊ2�ġ�O2��Բ��O2����ֱ��l�ϣ����ڡ�O1�ϣ���P��Բ��P��ֱ��l�ϣ��ҡ�P���O1����O2�����У����P�İ뾶Ϊ3��5��
��ͼ���뾶Ϊ4�ġ�O1��Բ��O1��ֱ��l�ϣ��뾶Ϊ2�ġ�O2��Բ��O2����ֱ��l�ϣ����ڡ�O1�ϣ���P��Բ��P��ֱ��l�ϣ��ҡ�P���O1����O2�����У����P�İ뾶Ϊ3��5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
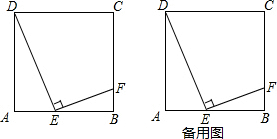
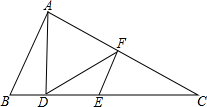 ��ͼ����ABC�У�AD��BC����B=2��C��E��F�ֱ���BC��AC���е㣬��DE=3�����߶�AB�ij���
��ͼ����ABC�У�AD��BC����B=2��C��E��F�ֱ���BC��AC���е㣬��DE=3�����߶�AB�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
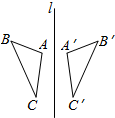 ��ͼ����ABC���A��B��C�����ֱ��l�Գƣ��ҡ�A=102�㣬��C��=25�㣬���B�Ķ���Ϊ��������
��ͼ����ABC���A��B��C�����ֱ��l�Գƣ��ҡ�A=102�㣬��C��=25�㣬���B�Ķ���Ϊ��������| A�� | 35�� | B�� | 53�� | C�� | 63�� | D�� | 43�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com