
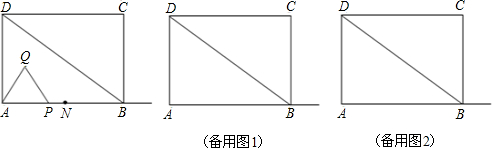
分析 (1)求出DQ,即可求出AP,即可得出答案,求出BP,求出AP即可;
(2)分为三种情况:画出图形,BM=MN,BN=MN.BM=BN,根据等腰三角形的性质求出即可.
(3)分为四种情况,画出图形,①0≤t≤8,②8<t≤12,③12<t<16,④t≥16,求出各个三角形的面积,根据图形即可得出答案.
解答 解: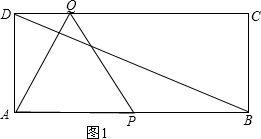 (1)如图1,当Q点在线段DC上时,
(1)如图1,当Q点在线段DC上时,
∵AD=4$\sqrt{3}$,∠ADQ=90°,∠DAQ=90°-60°=30°,
∴设DQ=x,则AQ=2x,
∴(4$\sqrt{3}$)2+x2=(2x)2,
解得:x=4,
∴AP=8,
∴t=8,
∴当t=8秒时,Q在线段DC上,
如图2: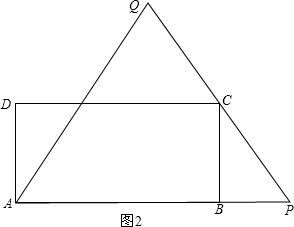 ∵当C在PQ上时,点P在AB延长线上,
∵当C在PQ上时,点P在AB延长线上,
由题意得:BP=$\frac{BC}{tan60°}$=$\frac{4\sqrt{3}}{\sqrt{3}}$=4,
∴AP=AB+BP=12+4=16,
∴t=16,
∴当t=16秒时,点C在线段PQ上.
(2)△BMN是等腰三角形,
分为三种情况:
①如图3,
当BN=MN时,
∵∠NMB=∠NBM=30°,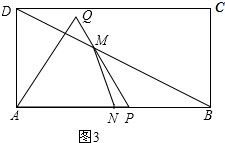
∴∠ANM=60°,
∴此时Q点在BD上,
P点与N重合,
∴AP=AN=6,
∴t=6;
②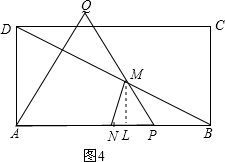 如图4,当BM=BN时,作ML⊥AB于L,
如图4,当BM=BN时,作ML⊥AB于L,
∵BM=BN,
∴BL=BM•cos30°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
ML=BM•sin30°=3,LP=$\sqrt{3}$,
BP=MP=2$\sqrt{3}$,
∴AP=12-2$\sqrt{3}$,
∴t=12-2$\sqrt{3}$;
③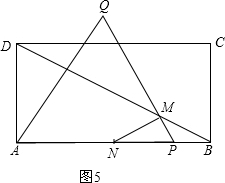 如图5,当BM=MN时,∠MNB=∠MBN=30°,
如图5,当BM=MN时,∠MNB=∠MBN=30°,
∵∠QPA=60°,
∴∠NMP=90°
∴BP=MP=$\frac{1}{2}$NP,
∴BP=2,AP=10,
∴t=10,
综合上述,当t=6秒或(12-2$\sqrt{3}$)秒或10秒时,
△BMN是等腰三角形.
(3)①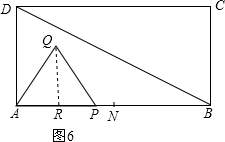 当0≤t≤8时,过Q作QR⊥AP于R,如图6所示:
当0≤t≤8时,过Q作QR⊥AP于R,如图6所示:
∵△APQ是等边三角形,
∴QA=QP=t,∠QAP=60°,
∴AR=PR=$\frac{1}{2}$t,
∴由勾股定理得:QR=$\frac{\sqrt{3}}{2}$t,
∴S=S△AQP=$\frac{1}{2}$×t×$\frac{\sqrt{3}}{2}$t,
即S=$\frac{\sqrt{3}}{4}$t2;
②如图7,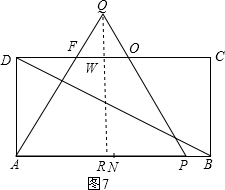 当8<t≤12时,
当8<t≤12时,
∵在Rt△ADF中,∠ADF=90°,∠DAF=90°-60°=30°,AD=4$\sqrt{3}$,
∴DF=AD×tan30°=4,
过Q作QR⊥AP于R,交DC于W,
∵四边形ABCD是矩形,
∴DC∥AB,
∴△QFO∽△QAP,
∴$\frac{FO}{AP}$=$\frac{QW}{QR}$,
∴$\frac{FO}{t}$=$\frac{\frac{\sqrt{3}}{2}t-4\sqrt{3}}{\frac{\sqrt{3}}{2}t}$,
∴FO=t-8,
∴S=S△APQ-S△QFO=$\frac{\sqrt{3}}{4}$t2-$\frac{1}{2}$(t-8)×$\frac{\sqrt{3}}{2}$(t-8),
S=4$\sqrt{3}$t-16$\sqrt{3}$;
③如图8,当12<t<16时,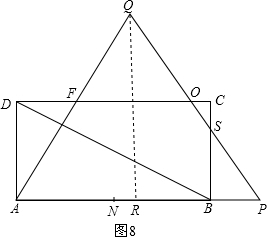 ∵BP=t-12,∠P=60°,
∵BP=t-12,∠P=60°,
∴BS=$\sqrt{3}$(t-12),
∴CS=4$\sqrt{3}$-$\sqrt{3}$(t-12)=16$\sqrt{3}$-$\sqrt{3}$t,
∵∠CSO=∠BSP=90°-60°=30°,
∴CO=$\frac{CS}{\sqrt{3}}$=16-t,
∴S=S△AQP-S△QFO-S△SBP
=$\frac{\sqrt{3}}{4}$t2-$\frac{1}{2}$(t-8)×$\frac{\sqrt{3}}{2}$(t-8)-$\frac{1}{2}$(t-12)×$\sqrt{3}$(t-12)
=-$\frac{\sqrt{3}}{2}$t2+16$\sqrt{3}$t-88$\sqrt{3}$;
④当t≥16时,如图9,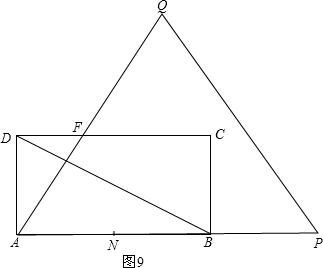 ∵Rt△ADF中,AD=4$\sqrt{3}$,∠DAF=90°-60°=30°,
∵Rt△ADF中,AD=4$\sqrt{3}$,∠DAF=90°-60°=30°,
∴DF=AD•tan30°=4,
∴S=S梯形CFAB=$\frac{1}{2}$×(CF+AB)×BC=$\frac{1}{2}$×(12-4+12)×4$\sqrt{3}$=40$\sqrt{3}$,
即S=40$\sqrt{3}$.
点评 本题是四边形综合题目,考查了三角形的面积、勾股定理、矩形的性质、等边三角形的性质和判定、三角函数等知识;题目比较好,综合性强,难度较大,用了分类讨论思想.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
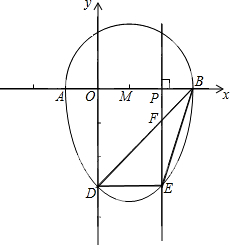 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
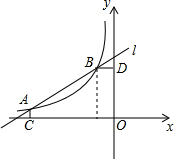 已知关于x的方程x2+2kx+k2-2k+1=0的两个实数根x1,x2满足x12=4-x22,反比例函数y=-$\frac{2k}{x}$的图象与直线l关于A(-4,m),B(-1,n)两点(如图),AC⊥x轴于C,BD⊥y轴于D.
已知关于x的方程x2+2kx+k2-2k+1=0的两个实数根x1,x2满足x12=4-x22,反比例函数y=-$\frac{2k}{x}$的图象与直线l关于A(-4,m),B(-1,n)两点(如图),AC⊥x轴于C,BD⊥y轴于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com