
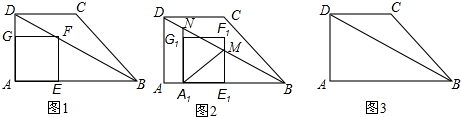
分析 (1)设AE=x,则EF=x,BE=6-x,证明△BEF∽△BAD,利用相似比得到$\frac{6-x}{6}$=$\frac{x}{3}$,然后根据比例性质求出x即可;
(2)①作MP⊥A1N于P,如图2,在Rt△ABD中利用勾股定理计算出BD=3$\sqrt{5}$,根据平移和矩形的性质易得MP=A1E1=2,再证明△MNP∽△BDA,则利用相似比可计算出MN=$\sqrt{5}$;
分类讨论:当MN=MA1=$\sqrt{5}$时,在Rt△A1E1M中利用勾股定理可计算出ME1=1,再证明△BME1∽△BDA,则利用相似比可计算出BE1=2,然后计算AA1即可得到对应s的值;当NM=NA1=$\sqrt{5}$时,利用△BNA1∽△BDA,可计算出BA1=2$\sqrt{5}$,则s=AA1=AB-BA1=6-2$\sqrt{5}$;当A1M=A1N时,作A1H⊥MN于H,如图2,根据等腰三角形的性质得NH=$\frac{1}{2}$MN=$\frac{\sqrt{5}}{2}$,证明△NHA1∽△DAB,利用相似比可计算出NA1=$\frac{5}{2}$,接着证明△BNA1∽△BDA,利用相似比计算出BA1=5,则s=AA1=1;
②作CI⊥AB于I,如图3(1),则AI=CD=3,而BI=AB-AI=3,则△BIC为等腰直角三角形,所以∠CBI=45°,当正方形,A1E1F1G1的顶点G1落在BC上时,如图3(1),通过证明△BG1A1∽△BDA,再利用相似比可计算出BA1=4,得到BE1=2,此时s=AA1=2,由于F1E1=2,则可判断F1点落在BC上,所以当2<s<4时,正方形A1E1F1G1与△BCD的重叠部分是五边形,如图3(2).
解答 (1)解:设AE=x,则EF=x,BE=6-x,
∵EF∥AD,
∴△BEF∽△BAD,
∴$\frac{BE}{BA}$=$\frac{EF}{AD}$,即$\frac{6-x}{6}$=$\frac{x}{3}$,解得x=2,
即线段AE的长为2;
(2)①证明:作MP⊥A1N于P,如图2,
在Rt△ABD中,BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
∵正方形AEFG沿AB向右平移得到正方形为A1E1F1G1,
∴MP=A1E1=2,
∵PM∥AB,
∴△MNP∽△BDA,
∴$\frac{MN}{BD}$=$\frac{MP}{BA}$,即$\frac{MN}{3\sqrt{5}}$=$\frac{2}{6}$,解得MN=$\sqrt{5}$,
∴在上述平移过程中,线段MN的长为定值;
当MN=MA1=$\sqrt{5}$时,在Rt△A1E1M中,ME1=$\sqrt{(\sqrt{5})^{2}-{2}^{2}}$=1,
∵ME1∥AD,
∴△BME1∽△BDA,
∴$\frac{B{E}_{1}}{BA}$=$\frac{M{E}_{1}}{AD}$,即$\frac{B{E}_{1}}{6}$=$\frac{1}{3}$,解得BE1=2,
∴s=AA1=6-2-2=2;
当NM=NA1=$\sqrt{5}$时,
∵NA1∥AD,
∴△BNA1∽△BDA,
∴$\frac{B{A}_{1}}{BA}$=$\frac{N{A}_{1}}{DA}$,即$\frac{B{A}_{1}}{6}$=$\frac{\sqrt{5}}{3}$,解得BA1=2$\sqrt{5}$,
∴s=AA1=6-2$\sqrt{5}$;
当A1M=A1N时,作A1H⊥MN于H,如图2,则NH=$\frac{1}{2}$MN=$\frac{\sqrt{5}}{2}$,
∵NA1∥AD,
∴∠A1NH=∠ADB,
∴△NHA1∽△DAB,
∴$\frac{N{A}_{1}}{DB}$=$\frac{NH}{DA}$,即$\frac{N{A}_{1}}{3\sqrt{5}}$=$\frac{\frac{\sqrt{5}}{2}}{3}$,解得NA1=$\frac{5}{2}$,
∵NA1∥AD,
∴△BNA1∽△BDA,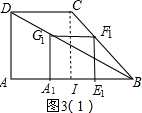
∴$\frac{B{A}_{1}}{BA}$=$\frac{N{A}_{1}}{DA}$,即$\frac{B{A}_{1}}{6}$=$\frac{\frac{5}{2}}{3}$,解得BA1=5,
∴s=AA1=6-5=1;
②作CI⊥AB于I,如图3(1),则AI=CD=3,而BI=AB-AI=6-3=3,
∴BI=CI,
∴△BIC为等腰直角三角形,
∴∠CBI=45°,
当正方形,A1E1F1G1的顶点G1落在BC上时,如图3(1),
∵G1A1∥AD,
∴△BG1A1∽△BDA,
∴$\frac{{G}_{1}{A}_{1}}{AD}$=$\frac{B{A}_{1}}{BA}$,即$\frac{2}{3}$=$\frac{B{A}_{1}}{6}$,解得BA1=4,
∴BE1=2,此时s=AA1=2,
而F1E1=2,
∴F1点落在BC上,
当正方形A1E1F1G1与△BCD的重叠部分是五边形时,2<s<4,如图3(2).
点评 本题考查了几何变换综合题:熟练掌握平移的性质、直角梯形和正方形的性质;灵活运用相似三角形的判定与性质计算线段的长;会利用分类讨论的思想解决数学问题;取特殊位置找到解决几何变换的突破口.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
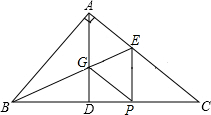 如图,在Rt△ABC中,AD是高线,BE平分∠ABC交AC于E,交AD于G,过E作EP⊥BC于P,连接GP,请问四边形AGPE是什么四边形?为什么?
如图,在Rt△ABC中,AD是高线,BE平分∠ABC交AC于E,交AD于G,过E作EP⊥BC于P,连接GP,请问四边形AGPE是什么四边形?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
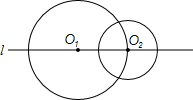 如图,半径为4的⊙O1的圆心O1在直线l上,半径为2的⊙O2的圆心O2既在直线l上,又在⊙O1上,⊙P的圆心P在直线l上,且⊙P与⊙O1、⊙O2都相切,则⊙P的半径为3或5.
如图,半径为4的⊙O1的圆心O1在直线l上,半径为2的⊙O2的圆心O2既在直线l上,又在⊙O1上,⊙P的圆心P在直线l上,且⊙P与⊙O1、⊙O2都相切,则⊙P的半径为3或5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com