
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
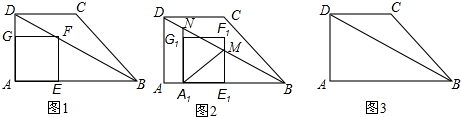
 已知关于x的方程x2+2kx+k2-2k+1=0的两个实数根x1,x2满足x12=4-x22,反比例函数y=-$\frac{2k}{x}$的图象与直线l关于A(-4,m),B(-1,n)两点(如图),AC⊥x轴于C,BD⊥y轴于D.
已知关于x的方程x2+2kx+k2-2k+1=0的两个实数根x1,x2满足x12=4-x22,反比例函数y=-$\frac{2k}{x}$的图象与直线l关于A(-4,m),B(-1,n)两点(如图),AC⊥x轴于C,BD⊥y轴于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
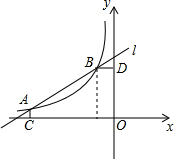
 在我国南方农村,常见到如图的屋顶,为防雨需在房顶铺上油毡,已知AB=AC,AD为△ABC的中线,且AD=3m,BC=8m,CE=10m,问需要用油毡多少平方米?
在我国南方农村,常见到如图的屋顶,为防雨需在房顶铺上油毡,已知AB=AC,AD为△ABC的中线,且AD=3m,BC=8m,CE=10m,问需要用油毡多少平方米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
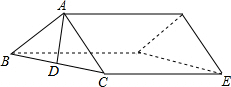
 如图所示,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s,连接PQ、AQ、CP,设点P、Q运动的时间为t s.当t为何值时,四边形ABQP是矩形?
如图所示,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s,连接PQ、AQ、CP,设点P、Q运动的时间为t s.当t为何值时,四边形ABQP是矩形?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
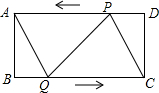
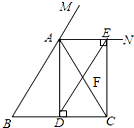 已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com