
【题目】在正方形ABCD中,DE为正方形的外角∠ADF的角平分线,点G在线段AD上,过点G作PG⊥DE于点P,连接CP,过点D作DQ⊥PC于点Q,交射线PG于点H.
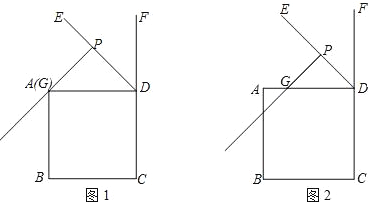
(1)如图1,若点G与点A重合.
①依题意补全图1;
②判断DH与PC的数量关系并加以证明;
(2)如图2,若点H恰好在线段AB上,正方形ABCD的边长为1,请写出求DP长的思路(可以不写出计算结果).
【答案】(1)①补图见解析;②DH=PC,证明见解析;(2)解法见解析.
【解析】
试题分析:(1)①依题意补全图形即可;
②由正方形的性质和角平分线得出∠EDF=∠ADE=45°,证出∠HAD=∠PDC,∠ADQ=∠DCQ,由ASA证明△HAD≌△PDC,得出对应边相等即可;
(2)思路如下:a、与②同理可证∠HGD=∠PDC,∠ADQ=∠DCP,可证△HGD∽△PDC;b、由②可知△GPD为等腰直角三角形,可设DP=PG=x,则GD=![]() x,AG=1﹣
x,AG=1﹣![]() x,易证△AGH为等腰直角三角形,则GH=
x,易证△AGH为等腰直角三角形,则GH=![]() ﹣2x;c、由△HGD∽△PDC得出比例式,解方程即可求得DP的长.
﹣2x;c、由△HGD∽△PDC得出比例式,解方程即可求得DP的长.
试题解析:(1)①依题意补全图1,如图1所示:
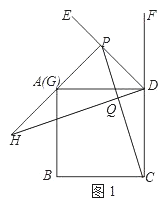
②DH=PC,理由如下:
∵DE为正方形的外角∠ADF的角平分线,
∴∠EDF=∠ADE=45°,
∵PG⊥DE于点P,
∴∠DAP=45°,
∴∠HAD=135°,∠PDC=135°,
∴∠HAD=∠PDC,
∵四边形ABCD为正方形,
∴AD=CD,
∵DQ⊥PC,
∴∠CDQ+∠DCQ=90°,
∵∠ADQ+∠CDQ=90°,
∴∠ADQ=∠DCQ,
在△HAD和△PDC中,
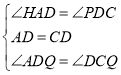 ,
,
∴△HAD≌△PDC(ASA),
∴DH=CP;
(2)求DP长的思路如下:如图2所示:
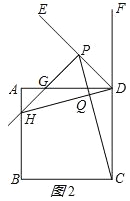
a、与②同理得:∠HGD=∠PDC,∠ADQ=∠DCP,
∴△HGD∽△PDC;
b、由②可知△GPD为等腰直角三角形,
∴∠AGH=∠PGD=45°,
∴△AGH为等腰直角三角形,
设DP=PG=x,则GD=![]() x,AG=1﹣
x,AG=1﹣![]() x,GH=
x,GH=![]() ﹣2x;
﹣2x;
c、由△HGD∽△PDC得:![]() ,
,
即![]() ,
,
解得:x=![]() (负值舍去),
(负值舍去),
∴DP=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,对称轴为x=1的抛物线经过A(﹣1,0),B(4,5)两点.
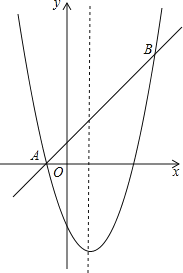
(1)求抛物线的解析式;
(2)P为直线AB上的动点,过点P作x轴的垂线交抛物线于点Q.
①当PQ=6时,求点P的坐标;
②是否存在点P,使以A、P、Q为顶点的三角形为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 和一次函数y=2x﹣1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.
和一次函数y=2x﹣1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.
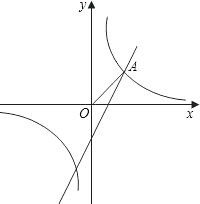
(1)求反比例函数的解析式;
(2)如图,已知点A在第一象限,且同时在上述两个函数的图象上,求点A的坐标;
(3)利用(2)的结果,请问:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( )
A.m>0,n>0 B.m>0,n<0
C.m<0,n>0 D.m<0,n<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:32-12=8×1;52-32=8×2;72-52=8×3;…,请用含正整数n的等式表示你所发现的规律:___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中记载了这样一道题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代的语言表述为:“如果AB为⊙O的直径,弦CD⊥AB于E,AE=1寸,CD=10寸,那么直径AB的长为多少寸?”请你补全示意图,并求出AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com