练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    ．如图，矩形ABCD中，BC=2，DC=4，以AB为直径的半圆O与DC相切于点E，则阴影部分的面积为多少？（结果保留π）

    　


    【考点】扇形面积的计算；切线的性质．

    【分析】连接OE．先求空白部分BCE的面积，再用△BCD的面积﹣空白部分BCE的面积得阴影面积．

    【解答】解：连接OE．

    阴影部分的面积=S△BCD﹣（S正方形OBCE﹣S扇形OBE）=×2×4﹣（2×2﹣π×2×2）=π．

    答：阴影部分的面积为π．

    【点评】本题考查了三角形的面积、矩形的性质、切线的性质的应用，关键是能把求不规则图形的面积转化成求规则图形的面积，题目比较典型，主要培养了学生的计算能力．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图所示的向日葵图案是用等分圆周画出的，则⊙O与半圆P的半径的比为（　　）

    A．2：1 B．4：1 C．3：1 D．5：3

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某新建火车站站前广场需要绿化的面积为46000米2，施工队在绿化了22000米2后，将每天的工作量增加为原来的1.5倍，结果提前4天完成了该项绿化工程．
    （1）该项绿化工程原计划每天完成多少米2？
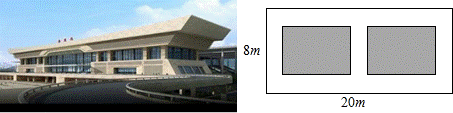
    （2）该项绿化工程中有一块长为20米，宽为8米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为56米2，两块绿地之间及周边留有宽度相等的人行通道（如图所示），问人行通道的宽度是多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    =　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （2x﹣3）2=x2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


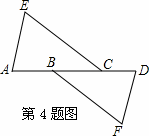
    如图，AE∥DF，AE=DF，要使△EAC≌△FDB，需要添加下列选项中的……（　　）

    A．AB=CD；  B．EC=BF；  C．∠A=∠D；    D．AB=BC；

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    4的算术平方根是           ，

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果一次函数y=kx+b的自变量在﹣2≤x≤6之间变化时，函数值是﹣11≤y≤9，试确定函数的关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


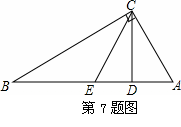
    如图，在Rt△ABC中，∠ACB=90°，CD为AB边上的高，若点A关于CD所在直线的对称点E恰好为AB的中点，则∠B的度数是…………………………………（　　）

    A．60° B．45° C．30° D．75°

     


    查看答案和解析>>

    同步练习册答案