
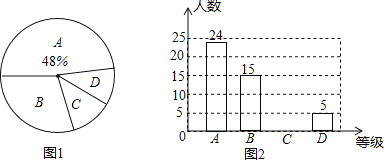
【题目】某销售公司年终进行业绩考核,人事部门把考核结果按照A,B,C,D四个等级,绘制成两个不完整的统计图,如图1,图2.
![]() 参加考试的人数是______,扇形统计图中D部分所对应的圆心角的度数是______,请把条形统计图补充完整;
参加考试的人数是______,扇形统计图中D部分所对应的圆心角的度数是______,请把条形统计图补充完整;
![]() 若公司领导计划从考核人员中选一人交流考核意见,求所选人员考核为A等级的概率;
若公司领导计划从考核人员中选一人交流考核意见,求所选人员考核为A等级的概率;
![]() 为推动公司进一步发展,公司决定计划两年内考核A等级的人数达到30人,求平均每年的增长率
为推动公司进一步发展,公司决定计划两年内考核A等级的人数达到30人,求平均每年的增长率![]() 精确到
精确到![]() ,
,![]()
【答案】(1)50,36;(2)![]() ;(3)12%.
;(3)12%.
【解析】
![]() 根据A等级的人数和所占的百分比求出总人数;用D等级所占的百分比乘以
根据A等级的人数和所占的百分比求出总人数;用D等级所占的百分比乘以![]() 即可求出D部分所对应的圆心角的度数;用总人数减去其它等级的人数,求出C等级的人数,从而补全统计图;
即可求出D部分所对应的圆心角的度数;用总人数减去其它等级的人数,求出C等级的人数,从而补全统计图;
![]() 用A等级的人数除以总人数即可得出所选人员考核为A等级的概率;
用A等级的人数除以总人数即可得出所选人员考核为A等级的概率;
![]() 设平均每年的增长率是x,根据两年内考核A等级的人数达到30人列出方程,然后求解即可.
设平均每年的增长率是x,根据两年内考核A等级的人数达到30人列出方程,然后求解即可.
解:![]() 参加考试的人数是:
参加考试的人数是:![]() 人;
人;
扇形统计图中D部分所对应的圆心角的度数是:![]() ;
;
C等级的人数是:![]() 人,补图如下:
人,补图如下: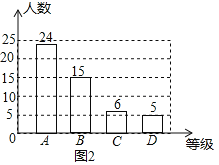
故答案为50,36;![]() 因为参考人数是50,考核为A等级的人数是24,
因为参考人数是50,考核为A等级的人数是24,![]() (考核为A等级)
(考核为A等级)![]() ;
;![]() 设增长率是x,依题意列方程得:
设增长率是x,依题意列方程得:![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
答:每年增长率为![]() .
.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
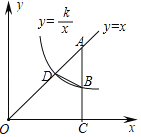
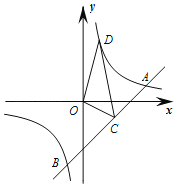
【题目】如图,直线y=x与反比例函数y=![]() (x>0)的图象相交于点D,点A为直线y=x上一点,过点A作AC⊥x轴于点C,交反比例函数y=
(x>0)的图象相交于点D,点A为直线y=x上一点,过点A作AC⊥x轴于点C,交反比例函数y=![]() (x>0)的图象于点B,连接BD.
(x>0)的图象于点B,连接BD.
(1)若点B的坐标为(8,2),则k= ,点D的坐标为 ;
(2)若AB=2BC,且△OAC的面积为18,求k的值及△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小安填写的数学实践活动报告的部分内容
题 目 | 测量铁塔顶端到地面的高度 | |
测量目标示意图 |
|
|
相关数据 | CD=20m,ɑ=45°,β=52° | |
求铁塔的高度FE(结果精确到1米)(参考数据:sin52°≈0.79, cos52°≈0.62,tan52°≈1.28)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 是常数)的图象与
是常数)的图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左边).
的左边).
(1)如果二次函数的图象经过原点.
①求![]() 的值;
的值;
②若![]() ,点
,点![]() 是一次函数
是一次函数![]() 图象上的一点,且
图象上的一点,且![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,函数的最大值为5,求
时,函数的最大值为5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
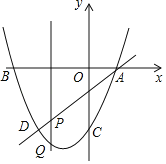
【题目】如图,抛物线y=ax2+bx﹣3过A(1,0),B(﹣3,0),直线AD交抛物线于点D,点D的横坐标为﹣2,点P(m,n)是线段AD上的动点.
(1)求直线AD及抛物线的解析式;
(2)过点P的直线垂直于x轴,交抛物线于点Q,求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平面内是否存在整点(横、纵坐标都为整数)R,使得P,Q,D,R为顶点的四边形是平行四边形?若存在,直接写出点R的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.

(1)发现:当正方形AEFG绕点A旋转,如图②所示.
①线段DG与BE之间的数量关系是 ;
②直线DG与直线BE之间的位置关系是 ;
(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由.
(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=x﹣3与双曲线y=![]() (k>0)交于A、B两点,点A的纵坐标为1.
(k>0)交于A、B两点,点A的纵坐标为1.
(1)求点B的坐标;
(2)直接写出当x在什么范围内时,代数式x2﹣3x的值小于k的值;
(3)点C(2,m)是直线AB上一点,点D(n,4)是双曲线y=![]() 上一点,将△OCD沿射线BA方向平移,得到△O′C′D′.若点O的对应点O′落在双曲线y=
上一点,将△OCD沿射线BA方向平移,得到△O′C′D′.若点O的对应点O′落在双曲线y=![]() 上,求点D的对应点D′的坐标.
上,求点D的对应点D′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四位同学在研究函数![]() (
(![]() 是常数)时,甲发现当
是常数)时,甲发现当![]() 时,函数有最小值;乙发现
时,函数有最小值;乙发现![]() 是方程
是方程![]() 的一个根;丙发现函数的最小值为3;丁发现当
的一个根;丙发现函数的最小值为3;丁发现当![]() 时,
时,![]() ,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A.甲B.乙C.丙D.丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com