
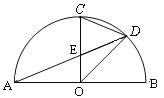
【题目】如图,AB是半圆直径,半径OC⊥AB于点O,点D是弧BC的中点,连结CD、AD、OD,给出以下四个结论:①∠DOB=∠ADC;②CE=OE;③△ODE∽△ADO;④2CD2=CE·AB.其中正确结论的序号是( )
A. ①③ B. ②④ C. ①②③ D. ①④
【答案】D
【解析】AB是半圆直径,
∴AO=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAO=![]() ∠CAB,
∠CAB,
∴∠CAD=∠ADO,
∴AC∥OD,
∴∠DOB=∠CAO,
又∵∠CAO=∠ADC(都对着半圆弧),
∴∠DOB=∠ADC故①正确;
②由题意得,OD=R,AC=![]() R,
R,
∵OE:CE=OD:AC=1: ![]() ,
,
∴OE≠CE,故②错误;
③∵在△ODE和△ADO中,只有∠ADO=∠EDO,
∵∠COD=2∠CAD=2∠OAD,
∴∠DEO≠∠DAO,
∴不能证明△ODE和△ADO相似,
∴③错误;
④∵AD平分∠CAB交弧BC于点D,
∴∠CAD=12×45°=22.5°,
∴∠COD=45°,
∵AB是半圆直径,
∴OC=OD,
∴∠OCD=∠ODC=67.5°
∵∠CAD=∠ADO=22.5°(已证),
∴∠CDE=∠ODC-∠ADO=67.5°-22.5°=45°,
∴△CED∽△COD,
∴CD2=ODCE=![]() ABCE,
ABCE,
∴2CD2=CEAB.
∴④正确.
故选D.


科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)化简:2a(a+b)﹣(a+b)2
(2)如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.试判断四边形OCED的形状,并说明理由. 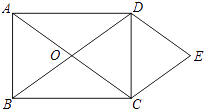
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A表示的数是﹣3,把点A向右移动5个单位,然再向左移动7个单位到A′,则A′表示的数是( )
A. ﹣5 B. ﹣6 C. ﹣7 D. ﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
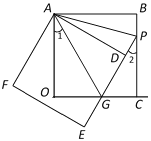
【题目】如图,将正方形ABCO绕点A顺时针旋转一定角度,得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
(1)求证:△AOG≌△ADG;
(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;
(3)若正方形ABCO的边长为![]() ,∠1=∠2,求AP的长.
,∠1=∠2,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
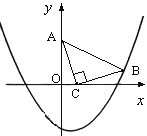
【题目】如图,在直角坐标系中,已知点A(0, 3)、点C(1, 0),等腰Rt△ACB的顶点B在抛物线![]() 上.
上.
(1)求点B的坐标及抛物线的解析式;
(2)在抛物线上是否存在点P(点B除外),使△ACP是以AC为直角边的Rt△?若存在,求出所有点P的坐标;若不存在,请说明理由.
(3)在抛物线上是否存在点Q(点B除外),使△ACQ是以AC为直角边的等腰Rt△?若存在直接写出所有点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com