
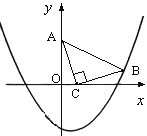
【题目】如图,在直角坐标系中,已知点A(0, 3)、点C(1, 0),等腰Rt△ACB的顶点B在抛物线![]() 上.
上.
(1)求点B的坐标及抛物线的解析式;
(2)在抛物线上是否存在点P(点B除外),使△ACP是以AC为直角边的Rt△?若存在,求出所有点P的坐标;若不存在,请说明理由.
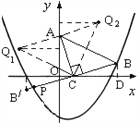
(3)在抛物线上是否存在点Q(点B除外),使△ACQ是以AC为直角边的等腰Rt△?若存在直接写出所有点Q的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)P2(
(2)P2(![]() 、 P3(
、 P3(![]() (3)不存在.
(3)不存在.
【解析】试题分析:(1)首先过点B作BD⊥x轴,垂足为D,易证得△BDC≌△COA,即可得BD=OC=1,CD=OA=2,则可求得点B的坐标;(2)利用待定系数法即可求得二次函数的解析式;(3)分别从①以AC为直角边,点C为直角顶点,则延长BC至点P1使得P1C=BC,得到等腰直角三角形ACP1,过点P1作P1M⊥x轴,②若以AC为直角边,点A为直角顶点,则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形ACP2,过点P2作P2N⊥y轴,③若以AC为直角边,点A为直角顶点,则过点A作AP3⊥CA,且使得AP3=AC,得到等腰直角三角形ACP3,过点P3作P3H⊥y轴,去分析则可求得答案.
试题解析:
(1)过B作BD⊥x轴,则△AOC≌△CDB,
∴B(4,1)
将B(4,1)代入![]() 得:
得: ![]()
(2)以C为直角顶点时P是BC与![]() 的交点,
的交点,
BC的解析式为![]() ; 解得P1(-1,-
; 解得P1(-1,- ![]() )(其中点B舍去)
)(其中点B舍去)
以A为直角顶点时,过A的直线平行于BC,∴易得解析式为![]() , 与抛物线交点:
, 与抛物线交点:
P2(![]()
![]() 、 P3(
、 P3(![]()
![]()
(3)不存在
理由:以C为直角顶点时,点B关于AC的对称点B/(―2,―1)不满足抛物线解析式
以A为直角顶点时,令AQ1=AC,求得Q1(―3,2) 不满足抛物线解析式
同理,当AQ2=AC时,求得Q2(3,4)不满足抛物线解析式


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是半圆直径,半径OC⊥AB于点O,点D是弧BC的中点,连结CD、AD、OD,给出以下四个结论:①∠DOB=∠ADC;②CE=OE;③△ODE∽△ADO;④2CD2=CE·AB.其中正确结论的序号是( )
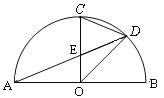
A. ①③ B. ②④ C. ①②③ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣1)2 ![]()
(2)[(﹣3a)2+3ab2c]2ab2
(3)(﹣ ![]() )100×3101
)100×3101
(4)(2a+b)(b﹣2a)﹣(a﹣3b)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2 . 
(1)图③可以解释为等式:
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图所示的块,块,块.
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下关系式:(1) ![]() (2)x+y=m(3)x2﹣y2=mn(4)
(2)x+y=m(3)x2﹣y2=mn(4) ![]() 其中正确的有
其中正确的有
A.1个
B.2个
C.3个
D.4个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第24秒时跳蚤所在位置的坐标是( )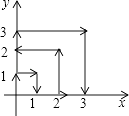
A.(0,3)
B.(4,0)
C.(0,4)
D.(4,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(结果保留根号) 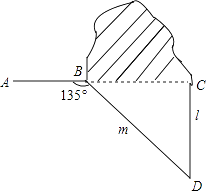
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com