
【题目】一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2 . 
(1)图③可以解释为等式:
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图所示的块,块,块.
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下关系式:(1) ![]() (2)x+y=m(3)x2﹣y2=mn(4)
(2)x+y=m(3)x2﹣y2=mn(4) ![]() 其中正确的有
其中正确的有
A.1个
B.2个
C.3个
D.4个.
【答案】
(1)(a+2b)(2a+b)=2a2+5ab+2b2
(2)2;7;3
(3)B
【解析】解:(1)图③可以解释为等式是(a+2b)(2a+b)=2a2+ab+4ab+2b2=2a2+5ab+2b2 , 故答案为:(a+2b)(2a+b)=2a2+5ab+2b2 . (2)(a+3b)(2a+b)=2a2+7ab+3b2 ,
故答案为:2,7,3.(3)∵m2﹣n2=4xy,∴(1)正确;
∵x+y=m,∴(2)正确;(3)(4)错误,
即正确的有2个,
故选B.
(1)求出长方形的长和宽,根据面积公式求出即可;(2)求出长方形的面积,即可得出答案;(3)根据长方形的长和宽,结合图形进行判断,即可得出选项.


科目:初中数学 来源: 题型:
【题目】综合题。
(1)化简:2a(a+b)﹣(a+b)2
(2)如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.试判断四边形OCED的形状,并说明理由. 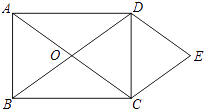
查看答案和解析>>
科目:初中数学 来源: 题型:
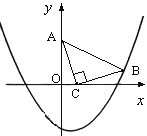
【题目】如图,在直角坐标系中,已知点A(0, 3)、点C(1, 0),等腰Rt△ACB的顶点B在抛物线![]() 上.
上.
(1)求点B的坐标及抛物线的解析式;
(2)在抛物线上是否存在点P(点B除外),使△ACP是以AC为直角边的Rt△?若存在,求出所有点P的坐标;若不存在,请说明理由.
(3)在抛物线上是否存在点Q(点B除外),使△ACQ是以AC为直角边的等腰Rt△?若存在直接写出所有点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com