
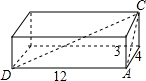
 一个长方体盒子,它的长是12dm,宽是4dm,高是3dm,
一个长方体盒子,它的长是12dm,宽是4dm,高是3dm,分析 (1)连接BD,先根据勾股定理求出BD2的值,再求出CD的长与12.5dm相比较即可;
(2)画出长方体盒子的平面展开图,利用勾股定理求解即可.
解答 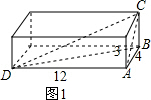 解:(1)如图1,连接BD,
解:(1)如图1,连接BD,
∵AD=12,AB=4,
∴BD2=AD2+AB2=122+42=160,
∴CD=$\sqrt{{BD}^{2}+{BC}^{2}}$=$\sqrt{160+{3}^{2}}$=13(dm).
∵13dm>12.5dm,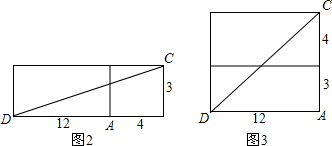 ∴长为12.5dm的铁棒能放进去;
∴长为12.5dm的铁棒能放进去;
(2)如图2所示,
CD=$\sqrt{(12+4)^{2}+{3}^{2}}$=$\sqrt{265}$dm.
如图3所示,CD=$\sqrt{{(3+4)}^{2}+{12}^{2}}$=$\sqrt{193}$dm,
∵$\sqrt{265}$>$\sqrt{193}$,
∴爬行的最短路程是$\sqrt{193}$dm.
点评 本题考查的是平面展开-最短路径问题,根据题意画出长方体的侧面展开图,利用勾股定理求解是解答此题的关键.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com