
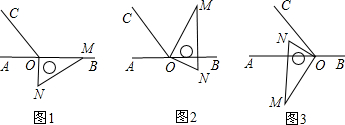
分析 (1)根据OM恰好平分∠BOC,用∠BOC的度数除以2,求出∠BOM的度数,即可求出∠AOM的度数是多少.
(2)首先根据∠AOM-∠NOC=30°,∠BOC=120°,求出∠A0C=60°,然后根据∠AON=90°-∠AOM=60°-∠NOC,判断出∠AOM与∠NOC之间满足什么等量关系即可.
(3)首先设三角板绕点O旋转的时间是x秒,根据∠BOC=120°,可得∠AOC=60°,∠BON=∠COD=30°;然后根据旋转60°时ON平分∠AOC,可得10x=60或10x=240,据此求出x的值是多少即可.
解答 解:(1)∵OM恰好平分∠BOC,
∴∠BOM=120°÷2=60°,
∴∠AOM=180°-120°=60°.
(2)如图3,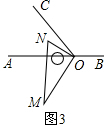 ,
,
∠AOM-∠NOC=30°,
∵∠BOC=120°,
∴∠A0C=60°,
∵∠AON=90°-∠AOM=60°-∠NOC,
∴∠AOM-∠NOC=30°.
(3)设三角板绕点O旋转的时间是x秒,
∵∠BOC=120°,
∴∠AOC=60°,
∴∠BON=∠COD=30°,
∴旋转60°时ON平分∠AOC,
∵10x=60或10x=240,
∴x=6或x=24,
即此时三角板绕点O旋转的时间是6或24秒.
故答案为:120、6或24.
点评 此题主要考查了角的计算,考查了分类讨论思想的应用,以及角平分线的性质和应用,要熟练掌握.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2-2x+3与x轴交于A、B两点,与y轴交于点C,M为抛物线的顶点,点P为x轴负半轴上一点,PC交AM于E,若AE=CE,求点P的坐标.
如图,抛物线y=-x2-2x+3与x轴交于A、B两点,与y轴交于点C,M为抛物线的顶点,点P为x轴负半轴上一点,PC交AM于E,若AE=CE,求点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{15}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{1}{12}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2x | B. | y=$\frac{1}{x}$+2 | C. | y=$\frac{1}{3}$-$\frac{1}{2}$x | D. | y=2x2-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com