
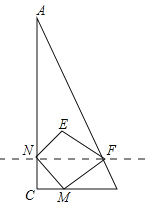
【题目】如图,已知△ABC中,∠C=90°,点M从点C出发沿CB方向以1cm/s的速度匀速运动,到达点B停止运动,在点M的运动过程中,过点M作直线MN交AC于点N,且保持∠NMC=45°,再过点N作AC的垂线交AB于点F,连接MF,将△MNF关于直线NF对称后得到△ENF,已知AC=8cm,BC=4cm,设点M运动时间为t(s),△ENF与△ANF重叠部分的面积为y(cm2).
(1)在点M的运动过程中,能否使得四边形MNEF为正方形?如果能,求出相应的t值;如果不能,说明理由;
(2)求y关于t的函数解析式及相应t的取值范围;
(3)当y取最大值时,求sin∠NEF的值.
【答案】(1)![]() ;(2)
;(2) ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)由已知得出CN=CM=t,FN∥BC,得出AN=8﹣t,由平行线证出△ANF∽△ACB,得出对应边成比例求出NF=![]() AN=
AN=![]() (8﹣t),由对称的性质得出∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,由正方形的性质得出OE=ON=FN,得出方程,解方程即可;
(8﹣t),由对称的性质得出∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,由正方形的性质得出OE=ON=FN,得出方程,解方程即可;
(2)分两种情况:①当0<t≤2时,由三角形面积得出![]() ;
;
②当2<t≤4时,作GH⊥NF于H,由(1)得:NF=![]() (8﹣t),GH=NH,GH=2FH,得出GH=
(8﹣t),GH=NH,GH=2FH,得出GH=![]() NF=
NF=![]() (8﹣t),由三角形面积得出
(8﹣t),由三角形面积得出![]() (2<t≤4);
(2<t≤4);
(3)当点E在AB边上时,y取最大值,连接EM,则EF=BF,EM=2CN=2CM=2t,EM=2BM,得出方程,解方程求出CN=CM=2,AN=6,得出BM=2,NF=![]() AN=3,因此EM=2BM=4,作FD⊥NE于D,由勾股定理求出EB=
AN=3,因此EM=2BM=4,作FD⊥NE于D,由勾股定理求出EB=![]() =
=![]() ,求出EF=
,求出EF=![]() EB=
EB=![]() ,由等腰直角三角形的性质和勾股定理得出DF=
,由等腰直角三角形的性质和勾股定理得出DF=![]() HF=
HF=![]() ,在Rt△DEF中,由三角函数定义即可求出sin∠NEF的值.
,在Rt△DEF中,由三角函数定义即可求出sin∠NEF的值.
试题解析:(1)能使得四边形MNEF为正方形;理由如下:
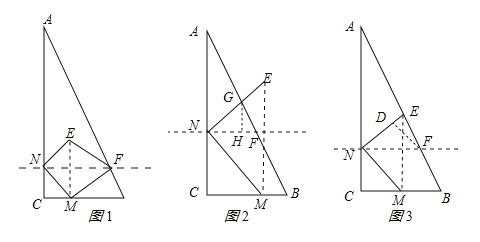
连接ME交NF于O,如图1所示:
∵∠C=90°,∠NMC=45°,NF⊥AC,∴CN=CM=t,FN∥BC,∴AN=8﹣t,△ANF∽△ACB,∴![]() =2,∴NF=
=2,∴NF=![]() AN=
AN=![]() (8﹣t),由对称的性质得:∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,∵四边形MNEF是正方形,∴OE=ON=FN,∴t=
(8﹣t),由对称的性质得:∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,∵四边形MNEF是正方形,∴OE=ON=FN,∴t=![]() ×
×![]() (8﹣t),解得:t=
(8﹣t),解得:t=![]() ;
;
即在点M的运动过程中,能使得四边形MNEF为正方形,t的值为![]() ;
;
(2)分两种情况:
①当0<t≤2时,y=![]() ×
×![]() (8﹣t)×t=
(8﹣t)×t=![]() ,即
,即![]() (0<t≤2);
(0<t≤2);
②当2<t≤4时,如图2所示:作GH⊥NF于H,由(1)得:NF=![]() (8﹣t),GH=NH,GH=2FH,∴GH=
(8﹣t),GH=NH,GH=2FH,∴GH=![]() NF=
NF=![]() (8﹣t),∴y=
(8﹣t),∴y=![]() NF′GH=
NF′GH=![]() ×
×![]() (8﹣t)×
(8﹣t)×![]() (8﹣t)=
(8﹣t)=![]() ,即
,即![]() (2<t≤4);
(2<t≤4);
综上所述: .
.
(3)当点E在AB边上时,y取最大值,连接EM,如图3所示:
则EF=BF,EM=2CN=2CM=2t,EM=2BM,∵BM=4﹣t,∴2t=2(4﹣t),解得:t=2,∴CN=CM=2,AN=6,∴BM=4﹣2=2,NF=![]() AN=3,∴EM=2BM=4,作FD⊥NE于D,则EB=
AN=3,∴EM=2BM=4,作FD⊥NE于D,则EB=![]() =
=![]() =
=![]() ,△DNF是等腰直角三角形,∴EF=
,△DNF是等腰直角三角形,∴EF=![]() EB=
EB=![]() ,DF=
,DF=![]() HF=
HF=![]() ,在Rt△DEF中,sin∠NEF=
,在Rt△DEF中,sin∠NEF=![]() =
=![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】据统计,甘肃省定西市2018年全市常住人口280.84万人,将数据280.84万用科学记数法表为( )
A. 2.8084×102B. 2.8084×104C. 2.8084×106D. 2.8084×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A(3,y1,),B(-2,y2)都在直线y=-2x+3上,则y1与y2的大小关系是( )
A. y1>y2 B. y2>y1 C. y1=y2 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
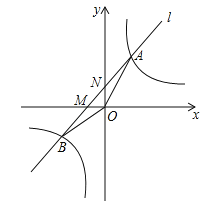
【题目】如图,设反比例函数的解析式为![]() (k>0).
(k>0).
(1)若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;
(2)若该反比例函数与过点M(﹣2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为![]() 时,求直线l的解析式.
时,求直线l的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为 km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com