
【题目】如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米.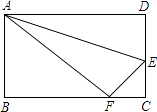
(1)BF=厘米;
(2)求EC的长.
【答案】
(1)6
(2)解:设EC=x厘米,则DE=(8-x)厘米,
由题意得EF=DE,FC=4厘米,∠C=900
由勾股定理得
![]()
![]()
解得 ![]()
答:EC长度为3厘米
【解析】(1)由图形翻折变换的性质可知,AD=AF=10,在Rt![]() ABF中,利用勾股定理即可求得BF的长;(2)设EC=x厘米,则DE=EF=8-x ,在Rt
ABF中,利用勾股定理即可求得BF的长;(2)设EC=x厘米,则DE=EF=8-x ,在Rt![]() CEF中,根据勾股定理列出方程求解即可.
CEF中,根据勾股定理列出方程求解即可.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
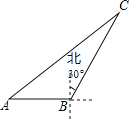
【题目】如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
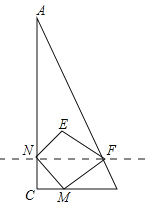
【题目】如图,已知△ABC中,∠C=90°,点M从点C出发沿CB方向以1cm/s的速度匀速运动,到达点B停止运动,在点M的运动过程中,过点M作直线MN交AC于点N,且保持∠NMC=45°,再过点N作AC的垂线交AB于点F,连接MF,将△MNF关于直线NF对称后得到△ENF,已知AC=8cm,BC=4cm,设点M运动时间为t(s),△ENF与△ANF重叠部分的面积为y(cm2).
(1)在点M的运动过程中,能否使得四边形MNEF为正方形?如果能,求出相应的t值;如果不能,说明理由;
(2)求y关于t的函数解析式及相应t的取值范围;
(3)当y取最大值时,求sin∠NEF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
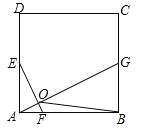
【题目】如图,在正方形ABCD中,点E、G分别是边AD、BC的中点,AF=![]() AB.
AB.
(1)求证:EF⊥AG;
(2)若点F、G分别在射线AB、BC上同时向右、向上运动,点G运动速度是点F运动速度的2倍,EF⊥AG是否成立(只写结果,不需说明理由)?
(3)正方形ABCD的边长为4,P是正方形ABCD内一点,当![]() ,求△PAB周长的最小值.
,求△PAB周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲数是x,比乙数少y,甲、乙两数之和与两数之差分别是( )
A. x+y、x﹣yB. 2x﹣y、2xC. 2x+y、﹣yD. 2x+y、x﹣y
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com