Question

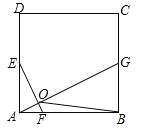
【题目】如图，在正方形ABCD中，点E、G分别是边AD、BC的中点，AF=AB．

（1）求证：EF⊥AG；

（2）若点F、G分别在射线AB、BC上同时向右、向上运动，点G运动速度是点F运动速度的2倍，EF⊥AG是否成立（只写结果，不需说明理由）？

（3）正方形ABCD的边长为4，P是正方形ABCD内一点，当，求△PAB周长的最小值．

Answer 1

【答案】（1）证明见解析；（2）成立；（3）．

【解析】

试题分析：（1）由正方形的性质得出AD=AB，∠EAF=∠ABG=90°，证出，得出△AEF∽△BAG，由相似三角形的性质得出∠AEF=∠BAG，再由角的互余关系和三角形内角和定理证出∠AOE=90°即可；

（2）证明△AEF∽△BAG，得出∠AEF=∠BAG，再由角的互余关系和三角形内角和定理即可得出结论；

（3）过O作MN∥AB，交AD于M，BC于N，则MN⊥AD，MN=AB=4，由三角形面积关系得出点P在线段MN上，当P为MN的中点时，△PAB的周长最小，此时PA=PB，PM=MN=2，连接EG，则EG∥AB，EG=AB=4，证明△AOF∽△GOE，得出 =，证出 =，得出AM=AE=，由勾股定理求出PA，即可得出答案．

试题解析：（1）证明：∵四边形ABCD是正方形，∴AD=AB，∠EAF=∠ABG=90°，∵点E、G分别是边AD、BC的中点，AF=AB，∴ =， =，∴，∴△AEF∽△BAG，∴∠AEF=∠BAG，∵∠BAG+∠EAO=90°，∴∠AEF+∠EAO=90°，∴∠AOE=90°，∴EF⊥AG；

（2）解：成立；理由如下：

根据题意得： =，∵ =，∴=，又∵∠EAF=∠ABG，∴△AEF∽△BAG，∴∠AEF=∠BAG，∵∠BAG+∠EAO=90°，∴∠AEF+∠EAO=90°，∴∠AOE=90°，∴EF⊥AG；

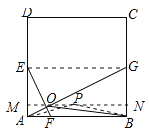
（3）解：过O作MN∥AB，交AD于M，BC于N，如图所示：

则MN⊥AD，MN=AB=4，∵P是正方形ABCD内一点，当S△PAB=S△OAB，∴点P在线段MN上，当P为MN的中点时，△PAB的周长最小，此时PA=PB，PM=MN=2，连接EG、PA、PB，则EG∥AB，EG=AB=4，∴△AOF∽△GOE，∴=，∵MN∥AB，∴ =，∴AM=AE=×2=，由勾股定理得：PA= =，∴△PAB周长的最小值=2PA+AB=．