
【题目】已知抛物线y=a(x﹣m)2+n与y轴交于点A,它的顶点为点B,点A、B关于原点O的对称点分别为C、D.若A、B、C、D中任何三点都不在一直线上,则称四边形ABCD为抛物线的伴随四边形,直线AB为抛物线的伴随直线.
(1)如图1,求抛物线y=(x﹣2)2+1的伴随直线的解析式.
(2)如图2,若抛物线y=a(x﹣m)2+n(m>0)的伴随直线是y=x﹣3,伴随四边形的面积为12,求此抛物线的解析式.
(3)如图3,若抛物线y=a(x﹣m)2+n的伴随直线是y=﹣2x+b(b>0),且伴随四边形ABCD是矩形.
①用含b的代数式表示m、n的值;
②在抛物线的对称轴上是否存在点P,使得△PBD是一个等腰三角形?若存在,请直接写出点P的坐标(用含b的代数式表示);若不存在,请说明理由.
【答案】
(1)
解:由抛物线y=a(x﹣m)2+n与y轴交于点A,它的顶点为点B,
∴抛物线y=(x﹣2)2+1的与y轴交于点A(0,5),它的顶点为点B(2,1),
设所求直线解析式为y=kx+b,
∴ ![]() ,
,
解得: ![]() ,
,
∴所求直线解析式为y=﹣2x+5
(2)
解:如图,作BE⊥AC于点E,由题意得四边形ABCD是平行四边形,
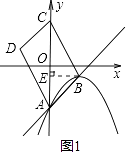
点A的坐标为(0,﹣3),
点C的坐标为(0,3),
可得:AC=6,
∵平行四边形ABCD的面积为12,
∴S△ABC=6即S△ABC= ![]() ACBE=6,
ACBE=6,
∴BE=2,
∵m>0,即顶点B在y轴的右侧,且在直线y=x﹣3上,
∴顶点B的坐标为(2,﹣1),
又抛物线经过点A(0,﹣3),
∴a=﹣ ![]() ,
,
∴y=﹣ ![]() (x﹣2)2﹣1
(x﹣2)2﹣1
(3)
解:①如图,作BF⊥x轴于点F,
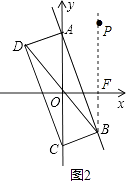
由已知可得A坐标为(0,b),C点坐标为(0,﹣b),
∵顶点B(m,n)在直线y=﹣2x+b(b>0)上,
∴n=﹣2m+b,即点B点的坐标为(m,﹣2m+b),
在矩形ABCD中,CO=BO.
∴b= ![]() ,
,
∴b2=m2+4m2﹣4mb+b2,
∴m= ![]() b,
b,
n=﹣2× ![]() b+b=﹣
b+b=﹣ ![]() b,
b,
②∵B点坐标为(m,n),即( ![]() b,﹣
b,﹣ ![]() b),
b),
∴BO= ![]() =b,
=b,
∴BD=2b,
当BD=BP,
∴PF=2b﹣ ![]() b=
b= ![]() b,
b,
∴P点的坐标为( ![]() b,
b, ![]() b);
b);
如图3,当DP=PB时,
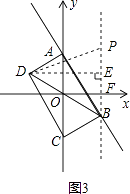
过点D作DE⊥PB,于点E,
∵B点坐标为( ![]() b,﹣
b,﹣ ![]() b),
b),
∴D点坐标为(﹣ ![]() b,
b, ![]() b),
b),
∴DE= ![]() b,BE=
b,BE= ![]() b,设PE=x,
b,设PE=x,
∴DP=PB= ![]() b+x,
b+x,
∴DE2+PE2=DP2,
∴ ![]() +x2=(
+x2=( ![]() b+x)2,
b+x)2,
解得:x= ![]() b,
b,
∴PF=PE+EF= ![]() b+
b+ ![]() b=
b= ![]() b,
b,
∴此时P点坐标为:( ![]() b,
b, ![]() b);
b);
同理P可以为( ![]() b,﹣
b,﹣ ![]() b);(
b);( ![]() b,
b, ![]() b),
b),
故P点坐标为:( ![]() b,
b, ![]() b);(
b);( ![]() b,
b, ![]() b);(
b);( ![]() b,﹣
b,﹣ ![]() b);(
b);( ![]() b,
b, ![]() b).
b).
【解析】(1)利用抛物线y=(x﹣2)2+1的与y轴交于点A(0,5),它的顶点为点B(2,1),求出直线解析式即可;(2)首先得出点A的坐标为(0,﹣3),以及点C的坐标为(0,3),进而求出BE=2,得出顶点B的坐标求出解析式即可;(3)①由已知可得A坐标为(0,b),C点坐标为(0,﹣b),以及n=﹣2m+b,即点B点的坐标为(m,﹣2m+b),利用勾股定理求出;②利用①中B点坐标,以及BD的长度即可得出P点的坐标.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人从![]() ,
, ![]() 两地同时出发,甲骑自行车,乙骑摩托车,沿同一条直线公路相向匀速行驶.出发后经
两地同时出发,甲骑自行车,乙骑摩托车,沿同一条直线公路相向匀速行驶.出发后经![]() 小时两人相遇.已知在相遇时乙比甲多行驶了
小时两人相遇.已知在相遇时乙比甲多行驶了![]() 千米,且摩托车的速度是自行车速度的
千米,且摩托车的速度是自行车速度的![]() 倍.
倍.
(1)问甲、乙行驶的速度分别是多少?
(2)甲、乙行驶多少小时,两车相距![]() 千米?
千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为Pn,则P2018的坐标是( )

A. (5,3) B. (3,5) C. (0,2) D. (2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B的坐标分别为A(-4,0)、B(2,0),点C在y轴上,且△ABC的面积为6,以点A、B、C为顶点作□ABCD.若过原点的直线平分该□ABCD的面积,则此直线的解析式是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为Pn,则P2018的坐标是( )

A. (5,3) B. (3,5) C. (0,2) D. (2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)2014年12月28日“青烟威荣”城际铁路正式开通,从烟台到北京的高铁里程比普快里程缩短了81千米,运行时间减少了9小时,已知烟台到北京的普快列车里程月1026千米,高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)某日王老师要去距离烟台大约630千米的某市参加14:00召开的会议,如果他买到
当日8:40从烟台到该是的高铁票,而且从该市火车站到会议地点最多需要1.5小时.试问在高铁列车准点到达的情况下他能在开会之前赶到吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】筹建中的城南中学需720套单人课桌椅(如图),光明厂承担了这项生产任务.该厂生产桌子必须5人一组.每组每天可生产12张;生产椅子必须4人一组,每组每天可生产24把.已知学校筹建组要求光明厂6天完成这项生产任务. 
(1)问光明厂平均毎天要生产多少套单人课桌椅?
(2)现学校筹建组要求至少提前1天完成这项生产任务.光明厂生产课桌椅的员工增加到84名,试给出一种分配生产桌子、椅子的员工数的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列材料来自2006年5月衢州有关媒体的真实报道:有关部门进行民众安全感满意度调查,方法是:在全市内采用等距抽样,抽取32个小区,共960户,每户抽一名年满16周岁并能清楚表达意见的人,同时,对比前一年的调查结果,得到统计图如下: 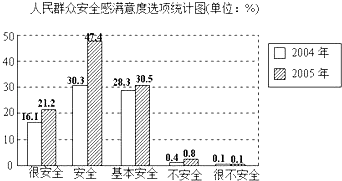
写出2005年民众安全感满意度的众数选项是;该统计图存在一个明显的错误是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com