
����Ŀ���ィ�еij�����ѧ��720���˿����Σ���ͼ�����������е��������������ó��������ӱ���5��һ�飮ÿ��ÿ�������12�ţ��������ӱ���4��һ�飬ÿ��ÿ�������24�ѣ���֪ѧУ�ィ��Ҫ�������6����������������� 
��1���ʹ�����ƽ������Ҫ�����������˿����Σ�
��2����ѧУ�ィ��Ҫ��������ǰ1������������������������������ε�Ա�����ӵ�84�����Ը���һ�ַ����������ӡ����ӵ�Ա�����ķ�����
���𰸡�
��1���⣺��720��6=120���ף���
�������ƽ������Ҫ����120���˿�����
��2���⣺��x���������ӣ���84��x�����������ӣ�
 ��
��
��ã�60��x��60��
��x=60��
��84��x=24��
��60���������ӣ�24����������
����������1����720���˿����Ρ�6�����������������=����Ҫ�������˿����ε���������2���ҵ��ؼ���������������ӵ�5��һ�飮ÿ��ÿ�������12�ţ����������ӵ�4��һ�飬ÿ��ÿ�������24�ѣ���������ǰ1��������������������ҵ���������Ĺ�ϵ���г�����ʽ����⣮
�����㾫�������ڱ��⿼���һԪһ�β���ʽ���Ӧ�ã���Ҫ�˽�1���������⣬�ҳ����ȹ�ϵ��2���裺��δ֪����3���У��г�����ʽ�飻4���⣺�ⲻ��ʽ�飻5�����飺�Ӳ���ʽ��Ľ⼯���ҳ���������Ĵ𰸣�6����д������𰸲��ܵó���ȷ�𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����ѧ����д���ֵ���������ǿ�������ӵ���ʶ��ijУ�ٰ�������������д��������ѧ����ѡ�κ�������������ͬʱ��д100�����֣�ÿ��ȷ��д��һ�����ֵ�1�֣����ξ�����ѧ���ɼ�Ϊ![]() ���֣�����
���֣�����![]() �����䰴�����η�Ϊ���飬���Ƴ����²���������
�����䰴�����η�Ϊ���飬���Ƴ����²���������
��� | �ɼ� | Ƶ���������� | Ƶ�� |
һ |
| 2 | 0.04 |
�� |
| 10 | 0.2 |
�� |
| 14 | b |
�� |
| a | 0.32 |
�� |
| 8 | 0.16 |
��1�����ξ������� ��ѧ���μӣ�
��2��ֱ��д������a= ,b= ;
��3���벹ȫ������Ӧ��Ƶ���ֲ�ֱ��ͼ��

��4���������ɼ�������80��Ϊ���㣬�δ�����������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=a��x��m��2+n��y�ύ�ڵ�A�����Ķ���Ϊ��B����A��B����ԭ��O�ĶԳƵ�ֱ�ΪC��D����A��B��C��D���κ����㶼����һֱ���ϣ�����ı���ABCDΪ�����ߵİ����ı��Σ�ֱ��ABΪ�����ߵİ���ֱ�ߣ�
��1����ͼ1����������y=��x��2��2+1�İ���ֱ�ߵĽ���ʽ��
��2����ͼ2����������y=a��x��m��2+n��m��0���İ���ֱ����y=x��3�������ı��ε����Ϊ12����������ߵĽ���ʽ��
��3����ͼ3����������y=a��x��m��2+n�İ���ֱ����y=��2x+b��b��0�����Ұ����ı���ABCD�Ǿ��Σ�
���ú�b�Ĵ���ʽ��ʾm��n��ֵ��
���������ߵĶԳ������Ƿ���ڵ�P��ʹ�á�PBD��һ�����������Σ������ڣ���ֱ��д����P�����꣨�ú�b�Ĵ���ʽ��ʾ�����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����2cm��������A��B��ֱ��l�ϣ����Ƿֱ���2cm/s��1cm/s���ٶ���l��ͬʱ����ƽ�ƣ�����A��B�ֱ�ƽ�Ƶ���A1 �� B1��λ��ʱ���뾶Ϊ1cm�ġ�A1 �� ��뾶ΪBB1�ġ�B���У����Aƽ�Ƶ���A1 �� ���õ�ʱ��Ϊs�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
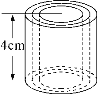
����Ŀ����ͼ��Բ���ĸ���4cm����Բ������뾶r(cm)�仯ʱ��Բ�������V(cm3)Ҳ��֮�仯��
(1)������仯�����У�д���Ա������������
(2) д��Բ�������V�����뾶r�Ĺ�ϵʽ��
(3)��Բ���ĵ���뾶��2cm�仯��8cmʱ��Բ��������ɶ���cm3�仯������cm3.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ͼ���У�����������ͼ���ܽ��Ƶؿ̻�����![]() �����龳��
�����龳��
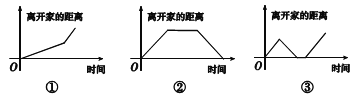
�龳![]() ��С���뿪�Ҳ��ã����ְ���ҵ�����ڼ�����Ƿ��ؼ����ҵ�����ҵ����ȥѧУ��
��С���뿪�Ҳ��ã����ְ���ҵ�����ڼ�����Ƿ��ؼ����ҵ�����ҵ����ȥѧУ��
�龳![]() ��С���Ӽҳ���������һ��·�̺�Ϊ�˸�ʱ�䣬�Ը�����ٶ�ǰ��.
��С���Ӽҳ���������һ��·�̺�Ϊ�˸�ʱ�䣬�Ը�����ٶ�ǰ��.
��1���龳![]() ��
�� ![]() ����Ӧ�ĺ���ͼ��ֱ�Ϊ������������������д��ţ���
����Ӧ�ĺ���ͼ��ֱ�Ϊ������������������д��ţ���
��2������Ϊʣ�µĺ���ͼ��д��һ���ʺϵ��龳��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB�ߵĴ�ֱƽ����l1��BC�ڵ�D��AC�ߵĴ�ֱƽ����l2��BC�ڵ�E��l1��l2�ཻ�ڵ�O������OA��OB��OC.
(1)����ADE���ܳ�Ϊ6 cm����OBC���ܳ�Ϊ16 cm.
�����߶�BC�ij���
�����߶�OA�ij���
(2)����BAC��120�������DAE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ�һֻ���ϴ�ԭ�������������������4����λ���ȵ����A��������������2����λ���ȵ����B��Ȼ��������������10����λ���ȵ����C��
��1���������������������ϱ�ʾ��A��B��C���㣻
��2�����ݵ�C�������ϵ�λ�ã���C���Կ��������ϴ�ԭ����������ĸ����������˼�����λ���ȵõ��ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B�����ô��������ô���֮����һ��������Բ�ο�����Ϊ�������������������Ҫ����A��B֮��ľ��룬�������������θ��Ӳ�����ֱ�Ӳ�����
(1)����������ѧ֪ʶ�����һ������A��B֮��ľ���ķ�������˵�����ɣ�
(2)������ƵIJ��������У���Ҫ������Щ���ݣ�Ϊʲô��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com