
分析 首先对该二次函数作出形状与性质的初步判断,该函数开口向上,求得对称轴,根据对称轴所在位置进行分三种情况分类讨论求得.
解答 解:∵抛物线的对称轴为x=$\frac{2}{2a}$=$\frac{1}{a}$,
①当对称轴x=$\frac{1}{a}$在-2≤x≤3上时,
∴当x=$\frac{1}{a}$时,y=-3,当x=-2时,y=6或当x=3时,y=6,
∴$\left\{\begin{array}{l}{-3=\frac{1}{a}-\frac{2}{a}+c}\\{6=4a+4+c}\end{array}\right.$或$\left\{\begin{array}{l}{-3=\frac{1}{a}-\frac{2}{a}+c}\\{6=9a-6+c}\end{array}\right.$,
解得a1=$\frac{1}{4}$(舍去),a2=1,a3=$\frac{15+\sqrt{189}}{18}$(舍去),x=$\frac{15-\sqrt{189}}{18}$(舍去),
∴a=1,c=-2,
∴a+c=-1;
②对称轴x=$\frac{1}{a}$在x<-2上;
当x=-2时,y=-3,x=3时,y=6,
∴$\left\{\begin{array}{l}{4a+4+c=-3}\\{9a-6+c=6}\end{array}\right.$
解得a=$\frac{19}{9}$(不合题意,舍去),
③对称轴x=$\frac{1}{a}$在x>3上,
当x=-2时,y=6,x=3时,y=-3,
∴$\left\{\begin{array}{l}{4a+4+c=6}\\{9a-6+c=-3}\end{array}\right.$,
解得a=$\frac{1}{5}$,c=$\frac{3}{4}$
∴a+c=$\frac{4}{5}$
故答案为-1或$\frac{4}{5}$.
点评 本题考查了二次函数的最值,本题主要考查对$\frac{1}{a}$与x取值范围得讨论,比较复杂,有一定难度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
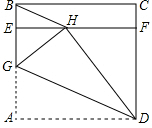 如图,ABCD是一张边长为4cm的正方形纸片,E、F分别为AB、CD上的点,且BE=CF,连接EF,沿过点D的直线将∠A翻折,使得点A落在EF上的点H处,折痕交AE于点G,当BH最短时,EG=4-4$\sqrt{2}$cm.
如图,ABCD是一张边长为4cm的正方形纸片,E、F分别为AB、CD上的点,且BE=CF,连接EF,沿过点D的直线将∠A翻折,使得点A落在EF上的点H处,折痕交AE于点G,当BH最短时,EG=4-4$\sqrt{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
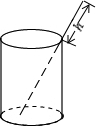 将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,如图,设筷子露在杯子外面的长度为h cm,则h的取值范围是( )
将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,如图,设筷子露在杯子外面的长度为h cm,则h的取值范围是( )| A. | h≤17 | B. | 7≤h≤16 | C. | 15≤h≤16 | D. | h≥8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com