
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬ ![]() ЦРЈ¬
ЦРЈ¬ ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() Ј®
Ј®


ЈЁ![]() Ј©өг
Ј©өг![]() ҙУөг
ҙУөг![]() ҝӘКјСШ
ҝӘКјСШ![]() ұЯПт
ұЯПт![]() ТФ
ТФ![]() өДЛЩ¶ИТЖ¶ҜЈ¬өг
өДЛЩ¶ИТЖ¶ҜЈ¬өг![]() ҙУ
ҙУ![]() өгҝӘКјСШ
өгҝӘКјСШ![]() ұЯПтөг
ұЯПтөг![]() ТФ
ТФ![]() өДЛЩ¶ИТЖ¶ҜЈ¬Из№ы
өДЛЩ¶ИТЖ¶ҜЈ¬Из№ы![]() Ј¬
Ј¬ ![]() ·ЦұрҙУ
·ЦұрҙУ![]() Ј¬
Ј¬ ![]() Н¬Кұіц·ўЈ¬ҫӯ№эјёГлЈ¬К№
Н¬Кұіц·ўЈ¬ҫӯ№эјёГлЈ¬К№![]() өДГж»эөИУЪ
өДГж»эөИУЪ![]() Јҝ
Јҝ
ЈЁ![]() Ј©өг
Ј©өг![]() ҙУөг
ҙУөг![]() ҝӘКјСШ
ҝӘКјСШ![]() ұЯПт
ұЯПт![]() ТФ
ТФ![]() өДЛЩ¶ИТЖ¶ҜЈ¬өг
өДЛЩ¶ИТЖ¶ҜЈ¬өг![]() ҙУ
ҙУ![]() өгҝӘКјСШ
өгҝӘКјСШ![]() ұЯПтөг
ұЯПтөг![]() ТФ
ТФ![]() өДЛЩ¶ИТЖ¶ҜЈ¬Из№ы
өДЛЩ¶ИТЖ¶ҜЈ¬Из№ы![]() Ј¬
Ј¬ ![]() ·ЦұрҙУ
·ЦұрҙУ![]() Ј¬
Ј¬ ![]() Н¬Кұіц·ўЈ¬ПЯ¶О
Н¬Кұіц·ўЈ¬ПЯ¶О![]() ДЬ·сҪ«
ДЬ·сҪ«![]() ·ЦіЙГж»эПаөИөДБҪІҝ·ЦЈҝИфДЬЈ¬ЗуіцФЛ¶ҜКұјдЈ»ИфІ»ДЬЛөГчАнУЙЈ®
·ЦіЙГж»эПаөИөДБҪІҝ·ЦЈҝИфДЬЈ¬ЗуіцФЛ¶ҜКұјдЈ»ИфІ»ДЬЛөГчАнУЙЈ®
ЈЁ![]() Ј©Иф
Ј©Иф![]() өгСШЙдПЯ
өгСШЙдПЯ![]() ·ҪПтҙУ
·ҪПтҙУ![]() өгіц·ўТФ
өгіц·ўТФ![]() өДЛЩ¶ИТЖ¶ҜЈ¬өг
өДЛЩ¶ИТЖ¶ҜЈ¬өг![]() СШЙдПЯ
СШЙдПЯ![]() ·ҪПтҙУ
·ҪПтҙУ![]() өгіц·ўТФ
өгіц·ўТФ![]() өДЛЩ¶ИТЖ¶ҜЈ¬
өДЛЩ¶ИТЖ¶ҜЈ¬ ![]() Ј¬
Ј¬ ![]() Н¬Кұіц·ўЈ¬ОКјёГләуЈ¬
Н¬Кұіц·ўЈ¬ОКјёГләуЈ¬ ![]() өДГж»эОӘ
өДГж»эОӘ![]() Јҝ
Јҝ
Ўҫҙр°ёЎҝЈЁ![]() Ј©ҫӯ№э
Ј©ҫӯ№э![]() Гл»т
Гл»т![]() ГләуЈ¬
ГләуЈ¬ ![]() Гж»эөИУЪ
Гж»эөИУЪ![]() Ј»ЈЁ
Ј»ЈЁ![]() Ј©І»ҙжФЪЈ¬АнУЙјыҪвОцЈ»ЈЁ
Ј©І»ҙжФЪЈ¬АнУЙјыҪвОцЈ»ЈЁ![]() Ј©
Ј©![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() КұЈ¬
КұЈ¬ ![]() Гж»эОӘ
Гж»эОӘ![]() .
.
ЎҫҪвОцЎҝКФМв·ЦОцЈәЈЁ1Ј©Йиҫӯ№э![]() ГлЈ¬К№
ГлЈ¬К№![]() Гж»эөИУЪ
Гж»эөИУЪ![]() Ј®ёщҫЭөИБҝ№ШПөЈә
Ј®ёщҫЭөИБҝ№ШПөЈә ![]() өДГж»эөИУЪ8cm2Ј¬БРіц·ҪіМЗуҪвјҙҝЙЈ»
өДГж»эөИУЪ8cm2Ј¬БРіц·ҪіМЗуҪвјҙҝЙЈ»
ЈЁ2Ј©Йиҫӯ№э![]() ГлЈ¬ПЯ¶О
ГлЈ¬ПЯ¶О![]() ДЬҪ«
ДЬҪ«![]() ·ЦіЙГж»эПаөИөДБҪІҝ·ЦёщҫЭГж»эЦ®јдөДөИБҝ№ШПөәНЕРұрКҪјҙҝЙЗуҪвЈ»
·ЦіЙГж»эПаөИөДБҪІҝ·ЦёщҫЭГж»эЦ®јдөДөИБҝ№ШПөәНЕРұрКҪјҙҝЙЗуҪвЈ»
ЈЁ3Ј©·ЦИэЦЦЗйҝцЈәўЩ![]() ФЪПЯ¶О
ФЪПЯ¶О![]() ЙПЈ¬
ЙПЈ¬ ![]() ФЪПЯ¶О
ФЪПЯ¶О![]() ЙПЈ¬
ЙПЈ¬ ![]() Ј¬ўЪ
Ј¬ўЪ![]() ФЪПЯ¶О
ФЪПЯ¶О![]() ЙПЈ¬
ЙПЈ¬ ![]() ФЪ
ФЪ![]() СУіӨПЯЙПЈ¬
СУіӨПЯЙПЈ¬ ![]() Ј®ўЫ
Ј®ўЫ![]() ФЪ
ФЪ![]() СУіӨПЯЙПЈ¬
СУіӨПЯЙПЈ¬ ![]() ФЪ
ФЪ![]() СУіӨПЯЙПЈ¬
СУіӨПЯЙПЈ¬ ![]() Ј¬ҪшРРМЦВЫјҙҝЙЗуҪвЈ®
Ј¬ҪшРРМЦВЫјҙҝЙЗуҪвЈ®
КФМвҪвОцЈәЈЁ![]() Ј©Йиҫӯ№э
Ј©Йиҫӯ№э![]() ГлЈ¬
ГлЈ¬
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬
№Кҫӯ№э![]() Гл»т
Гл»т![]() ГләуЈ¬
ГләуЈ¬ ![]() Гж»эөИУЪ
Гж»эөИУЪ![]() Ј®
Ј®
ЈЁ![]() Ј©Йиҫӯ№э
Ј©Йиҫӯ№э![]() ГлЈ¬
ГлЈ¬
![]() Гж»э
Гж»э![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
ЎаІ»ҙжФЪЈ®
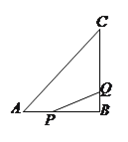
ЈЁ![]() Ј©ўЩ
Ј©ўЩ![]() ФЪПЯ¶О
ФЪПЯ¶О![]() ЙПЈ¬
ЙПЈ¬ ![]() ФЪПЯ¶О
ФЪПЯ¶О![]() ЙПЈ¬
ЙПЈ¬ ![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
ЎЯ![]() Ј¬
Ј¬
Ўа![]() Ј®
Ј®
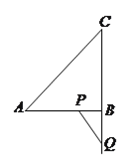
ўЪ![]() ФЪПЯ¶О
ФЪПЯ¶О![]() ЙПЈ¬
ЙПЈ¬ ![]() ФЪ
ФЪ![]() СУіӨПЯЙПЈ¬
СУіӨПЯЙПЈ¬ ![]() Ј®
Ј®
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() Ј®
Ј®
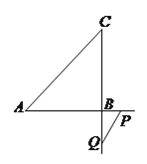
ўЫ![]() ФЪ
ФЪ![]() СУіӨПЯЙПЈ¬
СУіӨПЯЙПЈ¬ ![]() ФЪ
ФЪ![]() СУіӨПЯЙПЈ¬
СУіӨПЯЙПЈ¬ ![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
ЎЯ![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЧЫЙПЛщКцЈ¬ ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() КұЈ¬
КұЈ¬ ![]() Гж»эОӘ
Гж»эОӘ![]() .
.


 МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё
МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬Т»ҙОәҜКэy=kx+bөДНјПуУл·ҙұИАэәҜКэy=![]() ЈЁxЈҫ0Ј©өДНјПуҪ»УЪAЈЁ2Ј¬©Ғ1Ј©ЎўBЈЁ
ЈЁxЈҫ0Ј©өДНјПуҪ»УЪAЈЁ2Ј¬©Ғ1Ј©ЎўBЈЁ![]() Ј¬nЈ©БҪөгЈ®ЦұПЯy=2УлyЦбҪ»УЪөгCЈ®
Ј¬nЈ©БҪөгЈ®ЦұПЯy=2УлyЦбҪ»УЪөгCЈ®
1Ј©ЗуТ»ҙОәҜКэУл·ҙұИАэәҜКэөДҪвОцКҪЈ»
2Ј©ЗуЎчABCөДГж»эЈ»
3Ј©ЦұҪУРҙіцІ»өИКҪkx+bЈҫ![]() ФЪИзНјЛщКҫ·¶О§ДЪөДҪвјҜЈ®
ФЪИзНјЛщКҫ·¶О§ДЪөДҪвјҜЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФВөзҝЖјјУРПЮ№«ЛҫУГ160НтФӘЈ¬ЧчОӘРВІъЖ·өДСР·ў·СУГЈ¬іЙ№ҰСРЦЖіцБЛТ»ЦЦКРіЎјұРиөДөзЧУІъЖ·Ј¬ТСУЪөұДкН¶ИлЙъІъІўҪшРРПъКЫЈ®ТСЦӘЙъІъХвЦЦөзЧУІъЖ·өДіЙұҫОӘ4ФӘ/јюЈ¬ФЪПъКЫ№эіМЦР·ўПЦЈәГҝДкөДДкПъКЫБҝyЈЁНтјюЈ©УлПъКЫјЫёсxЈЁФӘ/јюЈ©өД№ШПөИзНјЛщКҫЈ¬ЖдЦРABОӘ·ҙұИАэәҜКэНјПуөДТ»Іҝ·ЦЈ¬BCОӘТ»ҙОәҜКэНјПуөДТ»Іҝ·ЦЈ®Й蹫ЛҫПъКЫХвЦЦөзЧУІъЖ·өДДкАыИуОӘsЈЁНтФӘЈ©Ј®ЈЁЧўЈәИфЙПТ»ДкУҜАыЈ¬ФтУҜАыІ»јЖИлПВТ»ДкөДДкАыИуЈ»ИфЙПТ»ДкҝчЛрЈ¬ФтҝчЛрјЖЧчПВТ»ДкөДіЙұҫЈ®Ј©
ЈЁ1Ј©ЗлЗуіцyЈЁНтјюЈ©УлxЈЁФӘ/јюЈ©Ц®јдөДәҜКэ№ШПөКҪЈ»
ЈЁ2Ј©ЗуіцөЪТ»ДкХвЦЦөзЧУІъЖ·өДДкАыИуsЈЁНтФӘЈ©УлxЈЁФӘ/јюЈ©Ц®јдөДәҜКэ№ШПөКҪЈ¬ІўЗуіцөЪТ»ДкДкАыИуөДЧоҙуЦөЈ®
ЈЁ3Ј©јЩЙ蹫ЛҫөДХвЦЦөзЧУІъЖ·өЪТ»ДкЗЎәГ°ҙДкАыИуsЈЁНтФӘЈ©ИЎөГЧоҙуЦөКұҪшРРПъКЫЈ¬ПЦёщҫЭөЪТ»ДкөДУҜҝчЗйҝцЈ¬ҫц¶ЁөЪ¶юДкҪ«ХвЦЦөзЧУІъЖ·ГҝјюөДПъКЫјЫёсxЈЁФӘЈ©¶ЁФЪ8ФӘТФЙПЈЁxЈҫ8Ј©Ј¬өұөЪ¶юДкөДДкАыИуІ»өНУЪ103НтФӘКұЈ¬ЗлҪбәПДкАыИуsЈЁНтФӘЈ©УлПъКЫјЫёсxЈЁФӘ/јюЈ©өДәҜКэКҫТвНјЈ¬ЗуПъКЫјЫёсxЈЁФӘ/јюЈ©өДИЎЦө·¶О§Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЈ¬ИзНјЈ¬ФЪЖҪРРЛДұЯРОABCDЦРЈ¬СУіӨDAөҪөгEЈ¬СУіӨBCөҪөгFЈ¬К№өГAEЈҪCFЈ¬Б¬ҪУEFЈ¬·ЦұрҪ»ABЈ¬CDУЪөгMЈ¬NЈ¬Б¬ҪУDMЈ¬BNЈ®
ЈЁ1Ј©ЗуЦӨЈәЎчAEMЎХЎчCFNЈ»
ЈЁ2Ј©ЗуЦӨЈәЛДұЯРОBMDNКЗЖҪРРЛДұЯРОЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіВГРРЙзТ»ФтВГУОПыПўИзПВЈә
ВГУОИЛКэ | КХ·СұкЧј |
І»і¬№э | ИЛҫщКХ·С |
і¬№э | ГҝФцјУТ»ИЛЈ¬ИЛҫщКХ·СјхЙЩ |
ЈЁ![]() Ј©јЧ№«ЛҫФұ№Ө·ЦБҪЕъІОјУёГПоВГУОЈ¬·ЦұрЦ§ё¶ёшВГРРЙз
Ј©јЧ№«ЛҫФұ№Ө·ЦБҪЕъІОјУёГПоВГУОЈ¬·ЦұрЦ§ё¶ёшВГРРЙз![]() ФӘәН
ФӘәН![]() ФӘЈ¬јЧ№«ЛҫФұ№ӨУР__________ИЛЈ®
ФӘЈ¬јЧ№«ЛҫФұ№ӨУР__________ИЛЈ®
ЈЁ![]() Ј©ТТ№«ЛҫФұ№ӨТ»ЖрІОјУёГПоВГУОЈ¬Ц§ё¶ёшВГРРЙз
Ј©ТТ№«ЛҫФұ№ӨТ»ЖрІОјУёГПоВГУОЈ¬Ц§ё¶ёшВГРРЙз![]() ФӘЈ¬ТТ№«ЛҫФұ№Ө¶аЙЩИЛЈҝ
ФӘЈ¬ТТ№«ЛҫФұ№Ө¶аЙЩИЛЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОӘБЛҫц¶ЁЛӯҪ«»сөГҪцУРөДТ»ХЕҝЖЖХұЁёжИліЎ„»Ј¬јЧәНТТЙијЖБЛИзПВөДГюЗтУОП·ЈәФЪІ»НёГчөДAЎўBБҪёцҝЪҙьЦР·Цұр·ЕИлұаәЕ·ЦұрОӘ1Ј¬2Ј¬3өДИэёцәмЗтј°Т»ёц°ЧЗтЈ¬ЛДёцРЎЗтіэБЛСХЙ«әНұаәЕІ»Н¬НвЈ¬ЖдЛыГ»УРИОәОЗшұрЈ»јЧФЪAҝЪҙьЦРГюіцБҪёцЗтЈ¬ТТФЪBҝЪҙьЦРГюіцТ»ёцЗтЈ¬Из№ыјЧГюіцөДБҪёцЗт¶јКЗәмЙ«өДјЧөГ1·ЦЈ¬·сФтЈ¬јЧөГ0·ЦЈ¬Из№ыТТГюіцөДЗтКЗ°ЧЙ«өДЈ¬ТТөГ1·ЦЈ¬·сФтТТөГ0·ЦЈ¬өГ·ЦёЯөД»сөГИліЎИҜЈ¬Из№ыөГ·ЦПаН¬Ј¬УОП·ЦШАҙЈ®
ЈЁ1Ј©ФЛУГБРұн»т»ӯКчЧҙНјөД·Ҫ·ЁЗујЧөГ1·ЦөДёЕВКЈ»
ЈЁ2Ј©ЗлДгУГЛщС§өДЦӘК¶ЛөГчХвёцУОП·КЗ·с№«ЖҪЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘЕЧОпПЯ![]() өД¶ҘөгCФЪxЦбХэ°лЦбЙПЈ¬Т»ҙОәҜКэ
өД¶ҘөгCФЪxЦбХэ°лЦбЙПЈ¬Т»ҙОәҜКэ![]() УлЕЧОпПЯҪ»УЪAЎўBБҪөгЈ¬УлxЎўyЦбҪ»УЪDЎўEБҪөгЈ®
УлЕЧОпПЯҪ»УЪAЎўBБҪөгЈ¬УлxЎўyЦбҪ»УЪDЎўEБҪөгЈ®

ЈЁ1Ј©ЗуmөДЦөЈ®
ЈЁ2Ј©ЗуAЎўBБҪөгөДЧшұкЈ®
ЈЁ3Ј©өгPЈЁaЈ¬bЈ©ЈЁ![]() Ј©КЗЕЧОпПЯЙПТ»өгЈ¬өұЎчPABөДГж»эКЗЎчABCГж»эөД2ұ¶КұЈ¬ЗуaЈ¬bөДЦөЈ®
Ј©КЗЕЧОпПЯЙПТ»өгЈ¬өұЎчPABөДГж»эКЗЎчABCГж»эөД2ұ¶КұЈ¬ЗуaЈ¬bөДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪАҘГчКР№мөАҪ»НЁөДРЮҪЁЦРЈ¬№ж»®ФЪAЎўBБҪөШРЮҪЁТ»¶ОөШМъЈ¬өгBФЪөгAөДХэ¶«·ҪПтЈ¬УЙУЪAЎўBЦ®јдҪЁЦюОпҪП¶аЈ¬ОЮ·ЁЦұҪУІвБҝЈ¬ПЦІвөГ№ЕКчCФЪөгAөДұұЖ«¶«45Ўг·ҪПтЙПЈ¬ФЪөгBөДұұЖ«Оч60Ўг·ҪПтЙПЈ¬BC=400mЈ¬ЗлДгЗуіцХв¶ОөШМъABөДіӨ¶ИЈ®ЈЁҪб№ыҫ«И·өҪ1mЈ¬ІОҝјКэҫЭЈә![]() Ј¬
Ј¬![]() Ј©
Ј©

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬өгMКЗЦұПЯy=2x+3ЙПөД¶ҜөгЈ¬№эөгMЧчMNҙ№ЦұУЪxЦбУЪөгNЈ¬yЦбЙПКЗ·сҙжФЪөгPЈ¬К№өГЎчMNPОӘөИСьЦұҪЗИэҪЗРОЈ¬Фт·ыәПМхјюөДөгPУРЈЁМбКҫЈәЦұҪЗИэҪЗРОРұұЯЙПөДЦРПЯөИУЪРұұЯөДТ»°лЈ©ЈЁЎЎЎЎЈ©

A. 2ёц B. 3ёц C. 4ёц D. 5ёц
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com