
【题目】某旅行社一则旅游消息如下:
旅游人数 | 收费标准 |
不超过 | 人均收费 |
超过 | 每增加一人,人均收费减少 |
(![]() )甲公司员工分两批参加该项旅游,分别支付给旅行社
)甲公司员工分两批参加该项旅游,分别支付给旅行社![]() 元和
元和![]() 元,甲公司员工有__________人.
元,甲公司员工有__________人.
(![]() )乙公司员工一起参加该项旅游,支付给旅行社
)乙公司员工一起参加该项旅游,支付给旅行社![]() 元,乙公司员工多少人?
元,乙公司员工多少人?
 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
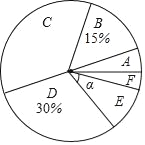
【题目】在星期一的第八节课,我校体育老师随机抽取了九年级的总分学生进行体育中考的模拟测试,并对成绩进行统计分析,绘制了频数分布表和统计图,按得分划分成A、B、C、D、E、F六个等级,并绘制成如下两幅不完整的统计图表.
等级 | 得分x(分) | 频数(人) |
A | 95<x≤100 | 4 |
B | 90<x≤95 | m |
C | 85<x≤90 | n |
D | 80<x≤85 | 24 |
E | 75<x≤80 | 8 |
F | 70<x≤75 | 4 |
请你根据图表中的信息完成下列问题:
1)本次抽样调查的样本容量是 .其中m= ,n= .
2)扇形统计图中,求E等级对应扇形的圆心角α的度数;
3)我校九年级共有700名学生,估计体育测试成绩在A、B两个等级的人数共有多少人?
4)我校决定从本次抽取的A等级学生(记为甲、乙、丙、丁)中,随机选择2名成为学校代表参加全市体能竞赛,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明购买了一套安居型商品房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:m),解答下列问题:
(1)用含x、y的代数式表示地面总面积;
(2)若x=5,y=![]() ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
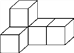
【题目】用5个相同的正方体搭出如图所示的组合体.
(1)分别画出从正面、左面、上面看这个组合体时看到的图形;
(2)如果在这个组合体中,再添加一个相同的正方体组成一个新组合体,从正面、左面看这个新组合体时,看到的图形与原来相同.你认为这个设想能实现吗?若能,画出添加正方体后,从上面看这个组合体时看到的图形;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人教版八年级下册第19章《一次函数》中“思考”:这两个函数的图象形状都是直线,并且倾斜程度相同,函数![]() 的图象经过原点,函数
的图象经过原点,函数![]() 的图象经与y轴交于点(0,5),即它可以看作直线
的图象经与y轴交于点(0,5),即它可以看作直线![]() 向上平移5个单位长度而得到。比较一次函数解析式
向上平移5个单位长度而得到。比较一次函数解析式![]()
![]() 与正比例函数解析式
与正比例函数解析式![]() ,容易得出:一次函数
,容易得出:一次函数![]()
![]() 的图象可由直线
的图象可由直线![]() 通过向上(或向下)平移
通过向上(或向下)平移![]() 个单位得到(当b>0时,向上平移,当b<0时,向下平移)。
个单位得到(当b>0时,向上平移,当b<0时,向下平移)。
(结论应用)一次函数![]() 的图象可以看作正比例函数 的图象向 平移 个单位长度得到;
的图象可以看作正比例函数 的图象向 平移 个单位长度得到;
(类比思考)如果将直线![]() 的图象向右平移5个单位长度,那么得到的直线的函数解析式是怎样的呢?我们可以这样思考:在直线
的图象向右平移5个单位长度,那么得到的直线的函数解析式是怎样的呢?我们可以这样思考:在直线![]() 上任意取两点A(0,0)和B(1,
上任意取两点A(0,0)和B(1,![]() ),将点A(0,0)和B(1,
),将点A(0,0)和B(1,![]() )向右平移5个单位得到点C(5,0)和D(6,
)向右平移5个单位得到点C(5,0)和D(6,![]() ),连接CD,则直线CD就是直线AB向右平移5个单位长度后得到的直线,设直线CD的解析式为:
),连接CD,则直线CD就是直线AB向右平移5个单位长度后得到的直线,设直线CD的解析式为:![]() ,将C(5,0)和D(6,
,将C(5,0)和D(6,![]() )代入得到:
)代入得到:![]() 解得
解得![]() ,所以直线CD的解析式为:
,所以直线CD的解析式为:![]() ;①将直线
;①将直线![]() 向左平移5个单位长度,则平移后得到的直线解析式为 .②若先将直线
向左平移5个单位长度,则平移后得到的直线解析式为 .②若先将直线![]() 向左平移4个单位长度后,再向上平移5个单位长度,得到直线
向左平移4个单位长度后,再向上平移5个单位长度,得到直线![]() ,则直线
,则直线![]() 的解析式为: .
的解析式为: .
(拓展应用)已知直线![]() :
:![]() 与直线关于x轴对称,求直线的解析式.
与直线关于x轴对称,求直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示, ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .
.


(![]() )点
)点![]() 从点
从点![]() 开始沿
开始沿![]() 边向
边向![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 点开始沿
点开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,如果
的速度移动,如果![]() ,
, ![]() 分别从
分别从![]() ,
, ![]() 同时出发,经过几秒,使
同时出发,经过几秒,使![]() 的面积等于
的面积等于![]() ?
?
(![]() )点
)点![]() 从点
从点![]() 开始沿
开始沿![]() 边向
边向![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 点开始沿
点开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,如果
的速度移动,如果![]() ,
, ![]() 分别从
分别从![]() ,
, ![]() 同时出发,线段
同时出发,线段![]() 能否将
能否将![]() 分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(![]() )若
)若![]() 点沿射线
点沿射线![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度移动,点
的速度移动,点![]() 沿射线
沿射线![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度移动,
的速度移动, ![]() ,
, ![]() 同时出发,问几秒后,
同时出发,问几秒后, ![]() 的面积为
的面积为![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:把对角线互相垂直的四边形叫做“正交四边形”.
如图1,在四边形![]() 中,
中,![]() ,四边形
,四边形![]() 就是“正交四边形”.
就是“正交四边形”.
(1)下列四边形,一定是“正交四边形”的是______.
①平行四边形②矩形③菱形④正方形
(2)如图2,在“正交四边形”![]() 中,点
中,点![]() 分别是边
分别是边![]() 的中点,求证:四边形
的中点,求证:四边形![]() 是矩形.
是矩形.
(3)小明说:“计算‘正交四边形’的面积可以仿照菱形的方法,面积是对角线之积的一半.”小明的说法正确吗?如果正确,请给出证明;如果错误,请给出反例.
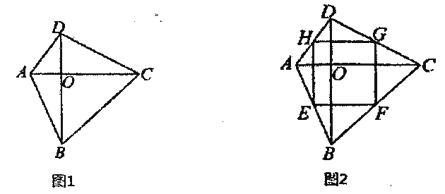
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.
(1)若△ABC以每秒2个单位的速度向右移动,⊙O不动,则经过多少时间△ABC的边与圆第一次相切?
(2)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,则经过多少时间△ABC的边与圆第一次相切?
(3)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,同时△ABC的边长AB、BC都以每秒0.5个单位沿BA、BC方向增大.△ABC的边与圆第一次相切时,点B运动了多少距离?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com