
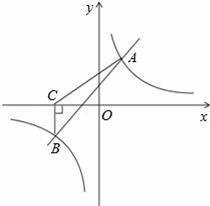
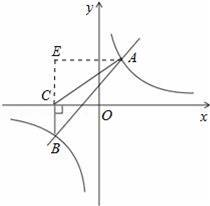
如图,一次函数y=kx+b与反比例函数y=
 的图象相交于A(2,3),B(﹣3,n)两点.
的图象相交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>
 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.

【考点】反比例函数与一次函数的交点问题.
【分析】(1)由一次函数y=kx+b与反比例函数y=
 的图象相交于A(2,3),B(﹣3,n)两点,首先求得反比例函数的解析式,则可求得B点的坐标,然后利用待定系数法即可求得一次函数的解析式;
的图象相交于A(2,3),B(﹣3,n)两点,首先求得反比例函数的解析式,则可求得B点的坐标,然后利用待定系数法即可求得一次函数的解析式;
(2)根据图象,观察即可求得答案;
(3)因为以BC为底,则BC边上的高为3+2=5,所以利用三角形面积的求解方法即可求得答案.
【解答】解:(1)∵点A(2,3)在y=
 的图象上,
的图象上,
∴m=6,
∴反比例函数的解析式为:y=
 ,
,
∵B(﹣3,n)在反比例函数图象上,
∴n=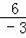
 =﹣2,
=﹣2,
∵A(2,3),B(﹣3,﹣2)两点在y=kx+b上,
∴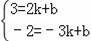
 ,
,
解得: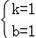
 ,
,
∴一次函数的解析式为:y=x+1;
(2)﹣3<x<0或x>2;
(3)以BC为底,则BC边上的高AE为3+2=5,
∴S△ABC=
 ×2×5=5.
×2×5=5.

【点评】此题考查了反比例函数与一次函数的交点问题.注意待定系数法的应用是解题的关键.


科目:初中数学 来源: 题型:
今年3月21日到武汉大学赏樱花的人数约为213000人,数213000用科学记数法表示为( )
A.21.3×104 B.213×103 C.2.13×105 D.2.13×104
查看答案和解析>>
科目:初中数学 来源: 题型:
某车的刹车距离y(m)与开始刹车时的速度x(m/s)之间满足二次函数y=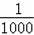
 x2+
x2+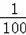
 x(x>0),若该车某次的刹车距离为9m,则开始刹车时的速度为 m/s.
x(x>0),若该车某次的刹车距离为9m,则开始刹车时的速度为 m/s.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com