
����Ŀ��С������Ҫ�øֹ����������������Ҫ��������Ҫ��Ϊ0.8�ĸֹ�100��������Ҫ��Ϊ2.5�ĸֹ�32�������ֳ��ȵĸֹܴ�ϸ������ͬ����Ҫ����Щ���ϲ����Ǻ��Ӷ��ɵģ����г����飬�ֲ��г��з������ֹ��ĸֹ�ÿ������Ϊ6�ף�
��1�����ʣ���һ����Ϊ6�ĸֹܽ��вü��������漸�ַ�����
��������(��������)��
�����٣�ֻ�ó�Ϊ0.8������ʱ�����ɲ�7����
�����ڣ��Ȳ���1��2.5�׳������ϣ����²�������ܲó�Ϊ0.8�׳������� ����
�����ۣ��Ȳ���2��2.5�׳������ϣ����²�������ܲó�Ϊ0.8�׳�������1 ����
��2���ֱ��ã�1���еķ����ںͷ����۸��ü����ٸ�6�׳��ĸֹܣ����ܸպõõ�����Ҫ����Ӧ�����IJ��ϣ�
��3����̽��������2���з����⣬�ڣ�1���л��������ַ������ϣ�����Ҫ6�׳��ĸֹ��루2���и�����ͬ��
���𰸡���1��4����2��24��4����3���������뷽��������
��������
��1����������ÿ����=�����Ϳ���ֱ�ӵó����ۣ�
��2�����÷����ڼ�x���������۲ü�y��6m���ĸֹܣ�����x+2y=32��4x+y=100���ɴ˷��̹��ɷ����������⼴�ɣ�
��3���ֱ��跽���ٲü�m���������۲ü�n��6m���ĸֹܺ��跽���ٲü�a���������ڲü�b��6m���ĸֹܣ����������������⼴�ɣ�
��1�� ��6-2.5����0.8=4��0.3�����ó�0.8�׳�������4����
�ʴ�Ϊ��4��
��2�� ���÷����ڼ�![]() ���������۲ü�
���������۲ü� ![]() ��6m���ĸֹܣ�
��6m���ĸֹܣ�
�����⣬��![]()
��ã�![]()
���÷����ڼ�![]() ���������۲ü�
���������۲ü�![]() ��
��![]() m���ĸֹܣ�
m���ĸֹܣ�
��3�� �跽���ٲü�![]() ���������۲ü�
���������۲ü�![]() ��
��![]() m���ĸֹܣ�
m���ĸֹܣ�
�����⣬��![]()
��ã�![]()
��m+n=28
![]() ��
��
![]()
�跽���ٲü� ![]() ���������ڲü�
���������ڲü� ![]() ��
��![]() m���ĸֹܣ�
m���ĸֹܣ�
�����⣬��![]()
��ã�![]() �����壬
�����壬
![]() �������뷽�������ϣ�����Ҫ
�������뷽�������ϣ�����Ҫ![]() m���ĸֹ��루
m���ĸֹ��루![]() ���и�����ͬ��
���и�����ͬ��


 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
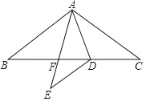
����Ŀ����ͼ������ABC�У���D��BC�ϣ�AB��AC��BD��AD��DC������ACD��AD�۵�����AED��AE��BC�ڵ�F��
��1�����C�Ķ�����
��2����֤��BF��CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���֪AB=8��BC=6��������ֱ�����������½ǵĶ���B������ת90����ͼ��λ�ã��������½ǵĶ������������ת90����ͼ��λ�á����Դ����ƣ�����������ת2018�κ���A��������ת��������������·��֮����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
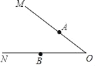
����Ŀ����ͼ����֪��MON����A��B�ֱ���OM��ON���ϣ���OA��OB��
��1������������A��B�ֱ���OM��ON�Ĵ��ߣ��������ߵĽ��������D��������ͼ�ۼ�����д��������
��2������OD������MON��50�������ODB���� ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���ڴ�����4����ȫ��ͬ��С�����Ƿֱ���Ϊ1��2��3��4�������ȡһ��С��Ȼ��Żأ����������ȡһ��С��
��1��������״ͼ�������б������г�������ȡС����ֵ����п��ܽ�������ش���ȡ������ֵ����Կ��ܽ�����м��֣�
��2����������ȡ��С������ͬ�ĸ��ʣ�
��3����������ȡ��С���ŵĺ͵���4�ĸ��ʣ�
��4����������ȡ��С���ŵĺ���2�ı�����3�ı����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ϵ�A��B��ʾ�ĵ�ֱ�Ϊ-6��3
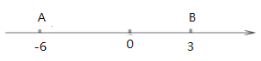
��1������������һ��P������A�͵�B�ľ�����ȣ����P��Ӧ��������________��ֱ��д���𰸣�
��2�������ʵ�����£�����Q�ӵ�P��������3����λ����/����ٶ��������������ƶ����Ƿ����ijһ��ʱ�̣�Q����B��ľ������ Q����A��ľ����2���������ڣ������Q�˶���ʱ�䣬�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ(ʮ��)�����ĸ���˿����������������ľ��Χ��һ��ľ������˿��С��������������˿�ľ�������Ϊ2��3��4��6����������ľ���ļнǾ��ɵ�����������ľ���ļн�ʱ���ƻ���ľ����������˿�ľ���֮���ֵΪ�Σ�

(A) 5 (B) 6 (C) 7 (D) 10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
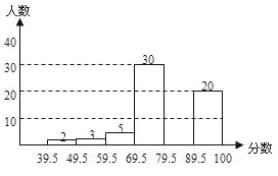
����Ŀ�����н�����꼶�������Խ�����ij��3000���ο�ѧ���г�ȡ��100�������ɼ�����ͳ�Ʒ���������100�֣��Ƿ־�Ϊ���������õ���ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ���������ͼ������������⣺
��1�������������������_________
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3����80�����ϣ���80�֣�Ϊ���㣬����ݴ˹�����ر��ο��Ե�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y= ![]() +bx��
+bx�� ![]() ��ͼ����x�ύ�ڵ�A����3��0���͵�B����ABΪ����x���Ϸ���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��
��ͼ����x�ύ�ڵ�A����3��0���͵�B����ABΪ����x���Ϸ���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��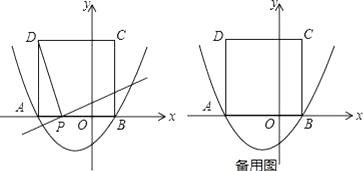
��1��b=����D�����꣺��
��2���߶�AO���Ƿ���ڵ�P����P����A��O�غϣ���ʹ��OE�ij�Ϊ1��
��3����x�Ḻ�������Ƿ���������ĵ�P��ʹ��PED�ǵ��������Σ������ڣ��������P�����꼰��ʱ��PED��������ABCD�ص����ֵ�������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com