【题目】如图，二次函数y= +bx﹣ 的图象与x轴交于点A（﹣3，0）和点B，以AB为边在x轴上方作正方形ABCD，点P是x轴上一动点，连接DP，过点P作DP的垂线与y轴交于点E．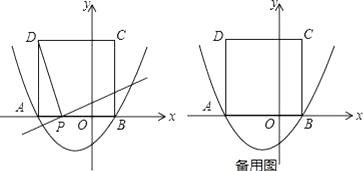

（1）b=；点D的坐标：；
（2）线段AO上是否存在点P（点P不与A、O重合），使得OE的长为1；
（3）在x轴负半轴上是否存在这样的点P，使△PED是等腰三角形？若存在，请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积；若不存在，请说明理由．

参考答案：

【答案】
（1）1,（﹣3,4）
（2）解：直线PE交y轴于点E，如图1，

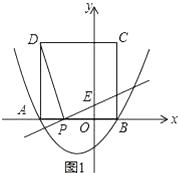
假设存在点P，使得OE的长为1，设OP=a，则AP=3﹣a，

∵DP⊥AE，∠APD+∠DPE+∠EPO=180°，

∴∠EPO=90°﹣∠APD=∠ADP，

tan∠ADP= = ，tan∠EPO= = ，

∴ = ，即 ﹣3a+4=0，

△= ﹣4×4=﹣7＜0，无解，

故线段AO上不存在点P（点P不与A、O重合），使得OE的长为1．


（3）解：假设存在这样的点P，DE交x轴于点M，如图2，

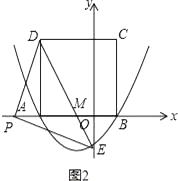
∵△PED是等腰三角形，

∴DP=PE，

∵DP⊥PE，四边形ABCD为正方形

∴∠EPO+∠APD=90°，∠DAP=90°，∠PAD+∠APD=90°，

∴∠EPO=∠PDA，∠PEO=∠DPA，

在△PEO和△DAP中，

∠EPO=∠PDA，DP=PE，∠PEO=∠DPA，

∴△PEO≌△DAP，

∴PO=DA=4，OE=AP=PO﹣AO=4﹣3=1，

∴点P坐标为（﹣4，0）．

∵DA⊥x轴，

∴DA∥EO，

∴∠ADM=∠OEM（两直线平行，内错角相等），

又∵∠AMD=∠OME（对顶角），

∴△DAM∽EOM，

∴ ，

∵OM+MA=OA=3，

∴MA= ×3= ，

△PED与正方形ABCD重叠部分△ADM面积为 ×AD×AM= ×4× = ．

答：存在这样的点P，点P的坐标为（﹣4，1），此时△PED与正方形ABCD重叠部分的面积为 ．


【解析】（1）∵点A（﹣3，0）在二次函数y= +bx﹣ 的图象上，

∴0= ﹣3b﹣ ，解得b=1，

∴二次函数解析式为y= +x﹣ = （x+3）（x﹣1），

∴点B（1，0），AB=1﹣（﹣3）=4，

∵四边形ABCD为正方形，

∴AD=AB=4，

∴点D（﹣3，4），

所以答案是：1；（﹣3，4）．

【考点精析】掌握正方形的性质和相似三角形的判定与性质是解答本题的根本，需要知道正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．

关闭