
����Ŀ����һ���ڴ�����4����ȫ��ͬ��С�����Ƿֱ���Ϊ1��2��3��4�������ȡһ��С��Ȼ��Żأ����������ȡһ��С��
��1��������״ͼ�������б������г�������ȡС����ֵ����п��ܽ�������ش���ȡ������ֵ����Կ��ܽ�����м��֣�
��2����������ȡ��С������ͬ�ĸ��ʣ�
��3����������ȡ��С���ŵĺ͵���4�ĸ��ʣ�
��4����������ȡ��С���ŵĺ���2�ı�����3�ı����ĸ��ʣ�
���𰸡�
��1���⣺����״ͼ�ã�
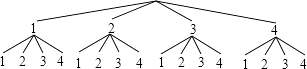
����16�ֵȿ��ܵĽ����
��2���⣺��������ȡ��С������ͬ����4�������
��������ȡ��С������ͬ�ĸ���Ϊ��4/16=1/4��
��3���⣺��������ȡ��С���ŵĺ͵���4����3�������
��������ȡ��С���ŵĺ͵���4�ĸ���Ϊ��3/16��
��4���⣺��������ȡ��С���ŵĺ���2�ı�����3�ı�������10�������
��������ȡ��С���ŵĺ���2�ı�����3�ı����ĸ���Ϊ��10/16=5/8��
����������1��ץס�ؼ�����֪�����������ȡһ��С��Ȼ��Żأ����������ȡһ��С���г���״ͼ��������п��ܵĽ�������ɡ�
��2�������������ȡ��С������ͬ����������ٸ��ݸ��ʹ�ʽ���㼴�ɡ�
��3�������������ȡ��С���ŵĺ͵���4����������ٸ��ݸ��ʹ�ʽ���㼴�ɡ�
��4�������������ȡ��С���ŵĺ���2�ı�����3�ı�������������ٸ��ݸ��ʹ�ʽ���㼴�ɡ�


 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ����� ![]() �У�
�� ![]() ��
�� ![]() ����
���� ![]() �ӵ�
�ӵ� ![]() ��������
�������� ![]() ���ٶ���
���ٶ��� ![]() ���
��� ![]() �˶������
�˶������ ![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ ![]() �룺
�룺 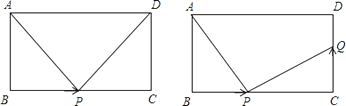
��1��![]()
![]() .(��
.(�� ![]() �Ĵ���ʽ��ʾ)
�Ĵ���ʽ��ʾ)
��2�� �� ![]() Ϊ��ֵʱ��
Ϊ��ֵʱ�� ![]()
��3������ ![]() �ӵ�
�ӵ� ![]() ��ʼ�˶���ͬʱ����
��ʼ�˶���ͬʱ���� ![]() �ӵ�
�ӵ� ![]() �������� v
�������� v![]() ���ٶ���
���ٶ��� ![]() ���
��� ![]() �˶����Ƿ����������v ֵ��ʹ��
�˶����Ƿ����������v ֵ��ʹ�� ![]() ȫ�ȣ������ڣ������ v��ֵ���������ڣ���˵������.
ȫ�ȣ������ڣ������ v��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ ![]() �У�
�У� ![]() ������ԭ�㡣��֪A(0,
������ԭ�㡣��֪A(0, ![]() )��B(1,0)��C��6,
)��B(1,0)��C��6, ![]() ������һ������ǡ�þ���������.
������һ������ǡ�þ���������.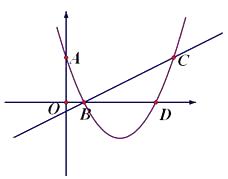
��1����������߽���ʽ��
��2���������߽� ![]() �����һ����ΪD����ô���������Ƿ����һ��P��ʹ��
�����һ����ΪD����ô���������Ƿ����һ��P��ʹ�� ![]() ,�����ڣ����P�����꣬�������ڣ���˵�����ɡ�
,�����ڣ����P�����꣬�������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�������� ![]() ��������ԭ�㣬�ҵ�
��������ԭ�㣬�ҵ� ![]() ʱ, y��x���������С.
ʱ, y��x���������С.
��1���������ߵĽ���ʽ��
��2������ͼ�����A�Ǹ���������λ��x���·���һ�����㣬����A��x���ƽ���߽�����������һ��D������AB ![]() x���ڵ�B, DC
x���ڵ�B, DC ![]() x���ڵ�C.
x���ڵ�C.
�ٵ� BC=1ʱ��ֱ��д������ABCD���ܳ���
���趯��A������Ϊ��a, b��,������ABCD���ܳ�L��ʾΪa�ĺ�������д���Ա�����ȡֵ��Χ���ж��ܳ��Ƿ�������ֵ��������ڣ����������ֵ���������ʱ��A�����ꣻ��������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�����У���ABC�Ķ��㶼�ڸ���ϣ���C����(0��-1)��
��1����������ABC ����ԭ��ԳƵġ�A1B1C1 �� ��д����A1�����ꣻ
�ڰѡ�ABC �Ƶ�C��ʱ����ת90�㣬�á�A2B2C2 �� ������A2B2C2 �� ��д����A2�����ꣻ
��2��ֱ��д����A2B2C2�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������Ҫ�øֹ����������������Ҫ��������Ҫ��Ϊ0.8�ĸֹ�100��������Ҫ��Ϊ2.5�ĸֹ�32�������ֳ��ȵĸֹܴ�ϸ������ͬ����Ҫ����Щ���ϲ����Ǻ��Ӷ��ɵģ����г����飬�ֲ��г��з������ֹ��ĸֹ�ÿ������Ϊ6�ף�
��1�����ʣ���һ����Ϊ6�ĸֹܽ��вü��������漸�ַ�����
��������(��������)��
�����٣�ֻ�ó�Ϊ0.8������ʱ�����ɲ�7����
�����ڣ��Ȳ���1��2.5�׳������ϣ����²�������ܲó�Ϊ0.8�׳������� ����
�����ۣ��Ȳ���2��2.5�׳������ϣ����²�������ܲó�Ϊ0.8�׳�������1 ����
��2���ֱ��ã�1���еķ����ںͷ����۸��ü����ٸ�6�׳��ĸֹܣ����ܸպõõ�����Ҫ����Ӧ�����IJ��ϣ�
��3����̽��������2���з����⣬�ڣ�1���л��������ַ������ϣ�����Ҫ6�׳��ĸֹ��루2���и�����ͬ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˳��з��㣬���ںܶ��ͥ��������С��������������Դ���źͻ���������ʯ�͵��г��۸�������Ϊ���ڼ۸�IJ����о����ܼ�����ʧ�����������ּ��ͷ�����
����һ��ÿ�μ�50Ԫ���ͣ���������ÿ�μ�50�����ͣ�
��ͬѧ����2�μ���Ϊ������һ���ͼ�ΪaԪ/�����ڶ����ͼ�ΪbԪ/����a��0��b��0��a��b�������������ַ����У����ּ��ͷ�����ʵ�ݱ��ˣ�ƽ������С�ı��ˣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2��bx��c(a��0)��ͼ����ͼ���Գ�����ֱ��x��1���������ĸ����ۣ�
��abc��0����b2��4ac��0����b����2a����a��b��c��2��������ȷ���� (��д���)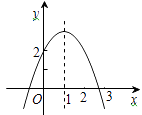
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˾Ͷ��750��Ԫ���ɹ����Ƴ�һ���г��������ϴ�IJ�Ʒ������Ͷ���ʽ�1750��Ԫ������������豸�ĸĽ�����֪���������У�ÿ����Ʒ�ijɱ�Ϊ60Ԫ�������۹����з��֣������۵��۶�Ϊ120Ԫʱ����������Ϊ24��������۵���ÿ����10Ԫ����������������1����������۵���Ϊx��Ԫ����x��120������������Ϊy�����������һ��������������=�����۶�����ɱ���Ϊz����Ԫ����
��1�����y��x֮�䣬z��x֮��ĺ�����ϵʽ��
��2���ù�˾�ܷ��ڵ�һ���ջ�Ͷ�ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com