练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在Rt△ABC中，∠ACB＝90°，AB＝4，AC＝2，则cosB＝         ．



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图16，E、F分别是等边三角形ABC的边AB、AC上的点，且BE=AF，CE、BF交于点P。

    （1）求证：CE=BF;

    （2）求∠BPC的度数

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，⊙O是△ABC的内切圆，切点分别为D、E、F，点M是⊙O上一点，∠EMF =55°，则∠A=       °．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


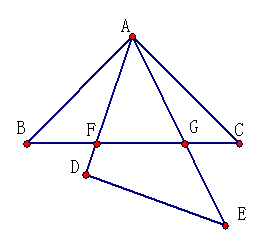
    如图△ABC与△DEA是两个全等的等腰直角三角形，∠BAC=∠D=90°，

    △DEA 绕点A旋转，边AD、AE与BC分别与AD、AE相交于点F、G ，CB = 5 ．

    回答下列问题：（共14分）

    （1）求证：△GAF∽△GBA  （3分）

    （2）求证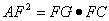：（3分）

    （3）设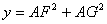,FG = x ,求y与x的函数关系式．

    （不要求写出自变量的取值范围）          （3分）

    （4）探究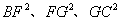之间的关系，证明你的结论． （5分）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知二次函数y＝ax2＋bx＋c（a≠0）的图象如图，则下列结论中正确的是（     ）

       A．ac>0； 　　　　　　　　　　　   B．当x>1时，y随x的增大而增大；

       C．2a＋b＝1； 　　　　　　　　　   D．方程ax2＋bx＋c＝0有一个根是x＝3。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


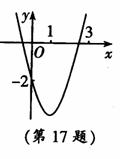
    如图，已知抛物线y＝x2＋bx＋c经过点（0，－2），请你确定

    一个b的值，使该抛物线与x轴的一个交点在(1，0)和(3，0)之间．

    你所确定的b的值为         ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    观察表格：

        根据表格解答下列问题：

        (1)a＝         ，b＝         ，c＝        ；

        (2)画出函数y＝ax2＋bx＋c的图象，并根据图象，直接

    写出当x取什么实数时，不等式ax2＋bx＋c>0成立．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若关于x的函数的图象与x轴只有一个公共点，则实数k的取值范围是             .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


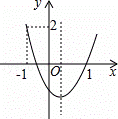
    如图，二次函数y=ax2+bx+c的图象开口向上，图象经过点（﹣1，2）和（1，0），且与y轴交于负半轴．给出四个结论：①abc＜0；②2a+b＞0；③a+b+c=0；④a＞0．其中正确的有(     )

        A．1个                  B．2个                  C．3个                  D．4个

    查看答案和解析>>

    同步练习册答案