
【题目】如图,抛物线y=﹣![]() (x+m)(x﹣4)(m>0)交x轴于点A、B(A左B右),交y轴于点C,过点B的直线y=
(x+m)(x﹣4)(m>0)交x轴于点A、B(A左B右),交y轴于点C,过点B的直线y=![]() x+b交y轴于点D.
x+b交y轴于点D.

(1)求点D的坐标;
(2)把直线BD沿x轴翻折,交抛物线第二象限图象上一点E,过点E作x轴垂线,垂足为点F,求AF的长;
(3)在(2)的条件下,点P为抛物线上一点,若四边形BDEP为平行四边形,求m的值及点P的坐标.
【答案】(1)D(0,﹣2);(2)AF=1;(3)m=3,P(2,5).
【解析】试题分析:(1)由点的直线上,点的坐标符合函数解析式,代入即可;
(2)先求出OB,OD再利用锐角三角函数求出BF=2EF,由它建立方程4-t=2×[-![]() (t+m)(t-4)],求解即可;
(t+m)(t-4)],求解即可;
(3)先判断出△PEQ≌△DBO,表示出点P(t+4,-![]() (t+m)(t-4))+2),再利用它在抛物线y=-
(t+m)(t-4))+2),再利用它在抛物线y=-![]() (t+m)(t-4)上求解.
(t+m)(t-4)上求解.
试题解析:(1)∵抛物线y=-![]() (x+m)(x-4)(m>0)交x轴于点A、B(A左B右)
(x+m)(x-4)(m>0)交x轴于点A、B(A左B右)
当y=0时,0=-![]() (x+m)(x-4),
(x+m)(x-4),
∴x1=-m,x2=4
∴A(-m,0),B(4,0)
∵点B在直线y=![]() x+b上,
x+b上,
∴4×![]() +b=0,b=-2
+b=0,b=-2
∴直线y=![]() x-2,
x-2,
当x=0时y=-2
∴D(0,-2),
(2)设E(t,-![]() (t+m)(t-4)),
(t+m)(t-4)),
∵EF⊥x轴,
∴∠EFO=90° EF∥y轴,
∴F(t,0),
由(1)可知D(0,-2)B(4,0),
∴OD=2 OB=4,
∴在Rt△BDO中,tan∠DBO=![]() ,
,
∵直线BD沿x轴翻折得到BE,
∴∠DBO=∠EBF,
∴tan∠DBO=tan∠EBF,
∴tan∠EBF=![]() ,
,
∴![]() ,
,
∴BF=2EF,
∴EF=-![]() (t+m)(t-4)BF=4-t
(t+m)(t-4)BF=4-t
∴4-t=2×[-![]() (t+m)(t-4)]
(t+m)(t-4)]
∴t+m=1,
∴AF=t-(-m)
∴AF=1,
(3)如图,
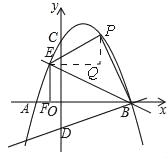
过点E作x轴的平行线,过点P作y轴的平行线交于点Q
设EP交y轴于点M
∵四边形BDEP是平行四边形
∴EP∥DB EP=DB
∵EP∥DB PQ∥y轴,
∴∠EMD=∠ODB∠EMD=∠EPQ,
∴∠ODB=∠EPQ,
∵∠PQE=∠DOB=90° EP=BD,
∴△PEQ≌△DBO,
∴PQ=OD=2 EQ=OB=4,
∵E(t,-![]() (t+m)(t-4)),
(t+m)(t-4)),
∴P(t+4,-![]() (t+m)(t-4)+2),
(t+m)(t-4)+2),
∵P(t+4,-![]() (t+m)(t-4))+2)在抛物线 y=-
(t+m)(t-4))+2)在抛物线 y=-![]() (t+m)(t-4)上
(t+m)(t-4)上
∴-![]() (t+4+m)(t+4-4)=-
(t+4+m)(t+4-4)=-![]() (t+m)(t-4)+2
(t+m)(t-4)+2
∵t+m=1,
∴t=-2,
∵t+m=1,
∴m=3,
∴-![]() (t+m)(t-4)+2=5,
(t+m)(t-4)+2=5,
∴P(2,5)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.
(1)请用直尺和圆规在图中直接作出∠A的平分线AE交BD于E;(不写作法,保留作图痕迹)
(2)在(1)的条件下,求出∠AED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
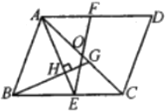
【题目】如图,在平行四边形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 是
是![]() 上一点,且
上一点,且![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,解答下列问题:
,解答下列问题:
①求证:![]() ;
;
②当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车同时从![]() 地前往
地前往![]() 地,甲车先到达
地,甲车先到达![]() 地,停留半小时后按原路返回.乙车的行驶速度为每小时50千米.如图所示是两车离出发点
地,停留半小时后按原路返回.乙车的行驶速度为每小时50千米.如图所示是两车离出发点![]() 地的距离
地的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)之间的函数图象.有下列说法:
(小时)之间的函数图象.有下列说法:
①![]() 、
、![]() 两地的距离是400千米;
两地的距离是400千米;
②甲车从![]() 到
到![]() 的行驶速度是每小时80千米;
的行驶速度是每小时80千米;
③甲车从![]() 到
到![]() 的行驶速度是每小时80千米;
的行驶速度是每小时80千米;
④两车相遇后1.6小时乙车到达![]() 地.
地.
其中正确的说法有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
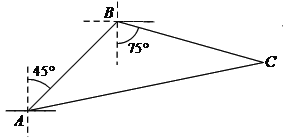
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱的高是![]() ,当圆柱的底面半径
,当圆柱的底面半径![]() 由小到大变化时,圆柱的体积
由小到大变化时,圆柱的体积![]() 也随之发生了变化.
也随之发生了变化.

(1)在这个变化中,自变量是______,因变量是______;
(2)写出体积![]() 与半径
与半径![]() 的关系式;
的关系式;
(3)当底面半径由![]() 变化到
变化到![]() 时,通过计算说明圆柱的体积增加了多少
时,通过计算说明圆柱的体积增加了多少![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与x轴交于点A、B(点A位于点B左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
与x轴交于点A、B(点A位于点B左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)设动点N(-2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上位于x轴上方的一点,请探究:是否存在点P,使以P、A、B为顶点的三角形与△ABD相似?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com