
����Ŀ���Ϸ�ij��ҵ����65�����������ס������ֲ�Ʒ��ÿ��ÿ������2����1���ң��ײ�Ʒÿ���ɻ���15Ԫ�������г�������������飬�Ҳ�Ʒÿ�����������5������ÿ������5��ʱ��ÿ���ɻ���120Ԫ��ÿ����1��������ƽ��ÿ���������2Ԫ����ÿ�찲��x�������Ҳ�Ʒ��
(1)������Ϣ�����
��Ʒ���� | ÿ�칤����(��) | ÿ�����(��) | ÿ����Ʒ�ɻ�����(Ԫ) |
�� | _______ | _________ | 15 |
�� | x | x | __________ |
(2)��ÿ�������ײ�Ʒ�ɻ�õ�����������Ҳ�Ʒ�ɻ�õ������550Ԫ����ÿ���Ҳ�Ʒ�ɻ�õ�����
(3)����ҵ�ڲ����ӹ��˵�����£�������������Ʒ��Ҫ��ÿ��ס������ֲ�Ʒ�IJ�����ȣ���֪ÿ��ÿ�������1����(ÿ��ÿ��ֻ������һ����Ʒ)������Ʒÿ���ɻ���30Ԫ����ÿ���������ֲ�Ʒ�ɻ�õ�������W(Ԫ)�����ֵ����Ӧ��xֵ��
���𰸡�(1) 65��x��2(65��x)��130��2x��(2) ÿ���Ҳ�Ʒ�ɻ�õ�������110Ԫ��(3) ����26�������Ҳ�Ʒʱ���ɻ�õ��������Ϊ3198Ԫ
��������
��1������������д������Ϣ���ɣ�
��2�����������г�������⼴�ɣ�
��3���������ײ�Ʒm�ˣ����������г����̿����m=![]() ���ٸ���x��m���ǷǸ��������ɵ�ȡx=26ʱ��m=13��65��x��m=26��
���ٸ���x��m���ǷǸ��������ɵ�ȡx=26ʱ��m=13��65��x��m=26��
��1����һ�� 65��x��2(65��x)���ڶ��� 130��2x��
��2��������15��2(65��x)=x(130��2x)+550,
��x2��80x+700=0
���x1=10��x2=70(�������⣬��ȥ)
��130��2x=110(Ԫ)��
��ÿ���Ҳ�Ʒ�ɻ�õ�������110Ԫ��
��3���������ײ�Ʒm�ˣ�
W=x(130��2x)+15��2m+30(65��x��m)=��2(x��25)2+3200,
��2m=65��x��m
��m=![]() ��
��
��x��m���ǷǸ�����
��ȡx=26ʱ��m=13��65��x��m=26,
����x=26ʱ��W���ֵ=3198��
�𣺰���26�������Ҳ�Ʒʱ���ɻ�õ��������Ϊ3198Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ƕ��壺�Խ����ഹֱ���ı��ν��������ı��Σ�

��1����ͼ1�������ı���ABCD�ĶԽ���AC��BD����O����֤��AB2+CD2��AD2+BC2��
��2����ͼ2���ֱ���Rt��ACB��ֱ�DZ�AC��б��ABΪ��������������ACFG��������ABDE������BE��CG��GE��
����֤���ı���BCGE�Ǵ����ı��Σ�
����AC��4��AB��5����GE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η���![]() ����������ȵ�ʵ������
����������ȵ�ʵ������
��1����m��ȡֵ��Χ��
��2����![]() ��
��![]() ��һԪ���η���
��һԪ���η���![]() ������������
������������![]() ����m��ֵ��
����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�ı߳�Ϊ2������B��ֱ��l��AB������ABC����A��BC������ֱ��l�Գƣ�DΪ�߶�BC����һ���㣬��AD��CD����Сֵ���� ��
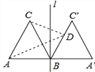
A. 4 B. 3![]() C. 2
C. 2![]() D. 2��
D. 2��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������� y��![]() ��ͼ����ͼ��ʾ������κ��� y =ax 2��2x��һ�κ��� y��bx+a ��ͬһƽ��ֱ������ϵ�е�ͼ������ǣ� ��
��ͼ����ͼ��ʾ������κ��� y =ax 2��2x��һ�κ��� y��bx+a ��ͬһƽ��ֱ������ϵ�е�ͼ������ǣ� ��
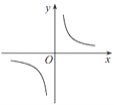
A.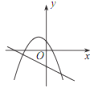 B.
B.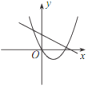 C.
C.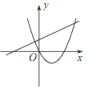 D.
D.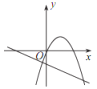
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y����2x��ͼ���뷴��������y��![]() ��ͼ���һ������ΪA(��1��n)
��ͼ���һ������ΪA(��1��n)
(1)��������y��![]() �ı���ʽ.
�ı���ʽ.
(2)��������ͼ�����һ����ΪB��ֱ��д��B������.
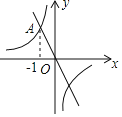
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У� ![]() ��
�� ![]() ������D���߶�BC�ϵĶ��㣬���߶�AD�Ƶ�A˳ʱ����ת50����
������D���߶�BC�ϵĶ��㣬���߶�AD�Ƶ�A˳ʱ����ת50����![]() ������
������![]() ����֪AB
����֪AB![]() 2cm����BDΪx cm��B
2cm����BDΪx cm��B![]() Ϊy cm��
Ϊy cm��

С������ѧϰ�����ľ��飬�Ժ���y���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����������С����̽�����̣��벹����������˵���������������ֵ������һλС����
��1��ͨ��ȡ�㡢��ͼ���������õ���![]() ��
��![]() �ļ���ֵ�����±���
�ļ���ֵ�����±���
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
��2������ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��

��3����ϻ����ĺ���ͼ������⣺
�߶�![]() �ij��ȵ���СֵԼΪ__________
�ij��ȵ���СֵԼΪ__________ ![]() ��
��
��![]()
![]() ����
����![]() �ij���x��ȡֵ��Χ��_____________��
�ij���x��ȡֵ��Χ��_____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڽ����ѧ����ʱ�����dz������������֣�������ۣ������Է��ֽ������IJ����뷽����
�����������
��֤�����һ����Բ���ڽ��ı��ζԽ����ഹֱ����ô����ı��εĶԱߵ�ƽ������һ����ֵ��
�����������֣�
���Dz����趨ԲO�İ뾶��R����O���ڽ��ı���ABCD�У�AC��BD��
������ͼ���в�ȫ������λ��ʱ��ͼ�Σ�������������ͼ��̽������Ľ��ۣ�

����������
��֪����ͼ�ڣ���Բ��O�İ뾶��R���ı���ABCD�ǡ�O���ڽ��ı��Σ� AC��BD��
��֤�� ��
֤����
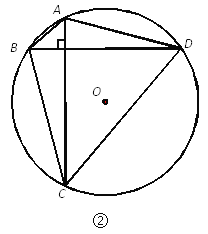
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=45������M��N�ڱ�OA�ϣ�OM=x��ON=x+4����P�DZ�OB�ϵĵ�.��ʹ��P��M��N���ɵ��������εĵ�Pǡ������������x��ֵ��________.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com