
【题目】我们定义:对角线互相垂直的四边形叫做垂美四边形.

(1)如图1,垂美四边形ABCD的对角线AC,BD交于O.求证:AB2+CD2=AD2+BC2;
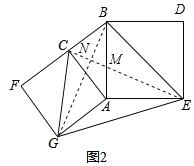
(2)如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结BE,CG,GE.
①求证:四边形BCGE是垂美四边形;
②若AC=4,AB=5,求GE的长.
【答案】(1)见解析;(2)①见解析;②GE=![]()
【解析】
(1)由垂美四边形得出AC⊥BD,则∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理得AD2+BC2=AO2+DO2+BO2+CO2,AB2+CD2=AO2+BO2+CO2+DO2,即可得出结论;
(2)①连接BG、CE相交于点N,CE交AB于点M,由正方形的性质得出AG=AC,AB=AE,∠CAG=∠BAE=90°,易求∠GAB=∠CAE,由SAS证得△GAB≌△CAE,得出∠ABG=∠AEC,由∠AEC+∠AME=90°,得出∠ABG+∠AME=90°,推出∠ABG+∠BMN=90°,即CE⊥BG,即可得出结论;
②垂美四边形得出CG2+BE2=CB2+GE2,由勾股定理得出BC=![]() =3,由正方形的性质得出CG=4
=3,由正方形的性质得出CG=4![]() ,BE=5
,BE=5![]() ,则GE2=CG2+BE2-CB2=73,即可得出结果.
,则GE2=CG2+BE2-CB2=73,即可得出结果.
(1)证明:∵垂美四边形ABCD的对角线AC,BD交于O,
∴AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得:AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AD2+BC2=AB2+CD2;
(2)①证明:连接BG、CE相交于点N,CE交AB于点M,如图2所示:
∵正方形ACFG和正方形ABDE,
∴AG=AC,AB=AE,∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
在△GAB和△CAE中,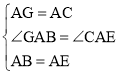 ,
,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,
∵∠AEC+∠AME=90°,
∴∠ABG+∠AME=90°,
∴∠ABG+∠BMN=90°,即CE⊥BG,
∴四边形BCGE是垂美四边形;
②解:∵四边形BCGE是垂美四边形,
∴由(1)得:CG2+BE2=CB2+GE2,
∵AC=4,AB=5,
∴BC=![]() =
=![]() =3,
=3,
∵正方形ACFG和正方形ABDE,
∴CG=![]() AC=4
AC=4![]() ,BE=
,BE=![]() AB=5
AB=5![]() ,
,
∴GE2=CG2+BE2﹣CB2=(4![]() )2+(5
)2+(5![]() )2﹣32=73,
)2﹣32=73,
∴GE=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数的图象与x轴的两个交点A,B关于直线x=﹣1对称,且AB=6,顶点在函数y=2x的图象上,则这个二次函数的表达式为________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
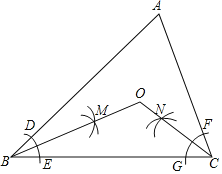
【题目】如图,在△ABC中,∠A=70°.按下列步骤作图:①分别以点B,C为圆心,适当长为半径画弧,分别交BA,BC,CA,CB于点D,E,F,G;②分别以点D,E为圆心,大于![]() DE为半径画弧,两弧交于点M;③分别以点F,G为圆心,大于
DE为半径画弧,两弧交于点M;③分别以点F,G为圆心,大于![]() FG为半径画弧,两弧交于点N;④作射线BM交射线CN于点O.则∠BOC的度数是_____.
FG为半径画弧,两弧交于点N;④作射线BM交射线CN于点O.则∠BOC的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
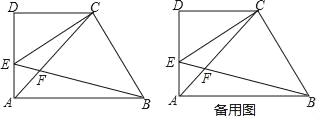
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在反比例函数y=﹣![]() 的图象上有一点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=![]() 的图象上运动,若tan∠CAB=3,则k=_____.
的图象上运动,若tan∠CAB=3,则k=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
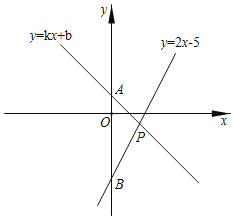
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(0,1),且与直线y=2x﹣5相交于点P,点P的横坐标为2,直线y=2x﹣5与y轴交于点B.
(1)求k、b的值;
(2)求△ABP的面积;
(3)根据图象可得,关于x的不等式2x﹣5>kx+b的解集是 ;
(4)若点Q在x轴上,且满足S△ABQ=S△ABP,则点Q的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
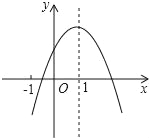
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列6个结论:
①abc<0;
②b<a﹣c;
③4a+2b+c>0;
④2c<3b;
⑤a+b<m(am+b),(m≠1的实数)
⑥2a+b+c>0,其中正确的结论的有_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com