
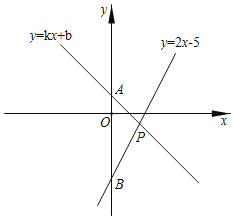
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(0,1),且与直线y=2x﹣5相交于点P,点P的横坐标为2,直线y=2x﹣5与y轴交于点B.
(1)求k、b的值;
(2)求△ABP的面积;
(3)根据图象可得,关于x的不等式2x﹣5>kx+b的解集是 ;
(4)若点Q在x轴上,且满足S△ABQ=S△ABP,则点Q的坐标是 .
【答案】(1)k=-1,b=1;(2)6;(3)x>2;(4)(2,0)或(﹣2,0).
【解析】
(1)利用待定系数法即可求k、b的值;
(2)求出点P的坐标即可求△ABP的面积;
(3)根据图象即可得关于x的不等式2x﹣5>kx+b的解集;
(4)分两种情况确定点Q在x轴上,且满足S△ABQ=S△ABP,即可求点Q的坐标.
解:(1)∵一次函数y=kx+b的图象经过点A(0,1),
∴b=1,
∵一次函数y=kx+b的图象与直线y=2x﹣5相交于点P,点P的横坐标为2,
∴点P的纵坐标为y=2×2﹣5=﹣1,
即P(2,﹣1),
把点P(2,﹣1)代入y=kx+1中,得k=﹣1,
答:k、b的值为﹣1、1;
(2)∵AB=6,P(2,﹣1).
∴S△ABP=![]() ×6×2=6.
×6×2=6.
答:△ABP的面积为6;
(3)∵一次函数y=kx+b的图象与直线y=2x﹣5相交于点P,点P的横坐标为2,
观察图象可知:
∴关于x的不等式2x﹣5>kx+b的解集是x>2;
故答案为x>2.
(4)∵点Q在x轴上,且满足S△ABQ=S△ABP,
∴S△ABQ=![]() ×6×OQ=6,
×6×OQ=6,
∴OQ=2,
则点Q的坐标是(2,0)或(﹣2,0).
故答案为:(2,0)或(﹣2,0).


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:初中数学 来源: 题型:
【题目】如图抛物线y=x2+bx﹣c经过直线y=x﹣3与坐标轴的两个交点A,B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)求S△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:对角线互相垂直的四边形叫做垂美四边形.

(1)如图1,垂美四边形ABCD的对角线AC,BD交于O.求证:AB2+CD2=AD2+BC2;
(2)如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结BE,CG,GE.
①求证:四边形BCGE是垂美四边形;
②若AC=4,AB=5,求GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
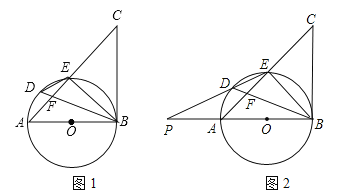
【题目】如图1,以△ABC的边AB为直径作⊙O,交AC边于点E,BD平分∠ABE交AC于F,交⊙O于点D,且∠BDE=∠CBE.
(1)求证:BC是⊙O的切线;
(2)延长ED交直线AB于点P,如图2,若PA=AO,DE=3,DF=2,求![]() 的值及AO的长.
的值及AO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
给出下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴在y轴的左侧;
③抛物线一定经过(3,0)点;
④在对称轴左侧y随x的增大而减增大.
从表中可知,其中正确的个数为( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐乐和数学小组的同学们研究了如下问题,请你也来试一下吧.
点![]() 是直线
是直线![]() 上一点,在同一平面内,乐乐他们把一个等腰直角三角板
上一点,在同一平面内,乐乐他们把一个等腰直角三角板![]() 任意放,其中直角顶点
任意放,其中直角顶点![]() 与点
与点![]() 重合,过点
重合,过点![]() 作直线
作直线![]() ,垂足为点
,垂足为点![]() ,从过点
,从过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
(1)当直线![]() ,
,![]() 位于点
位于点![]() 的异侧时,如图1,线段
的异侧时,如图1,线段![]() ,
,![]() ,
,![]() 之间的数量关系___(不必说明理由);
之间的数量关系___(不必说明理由);
(2)当直线![]() ,
,![]() 位于点
位于点![]() 的右侧时,如图2,判断线段
的右侧时,如图2,判断线段![]() ,
,![]() ,
,![]() 之间的数量系,并说明理由;
之间的数量系,并说明理由;
(3)当直线![]() ,
,![]() 位于点
位于点![]() 的左侧时,如图3,请你补全图形,并直接写出线段
的左侧时,如图3,请你补全图形,并直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发商以每件50元的价格购进400件T恤.若以单价70元销售,预计可售出200件.批发商的销售策略是:第一个月为增加销售量,降价销售,经过市场调查,单价每降低0.5元,可多售出5件,但最低单价不低于购进的价格;第一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元.设第一个月单价降低x元.
(1)根据题意,完成下表:
每件T恤的利润(元) | 销售量(件) | |
第一个月 | ||
清仓时 |
(2)T恤的销售单价定为多少元时,该批发商可获得最大利润?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com