【题目】如图，在平面直角坐标系xOy中，一次函数y＝﹣2x的图象与反比例函数y＝
的图象的一个交点为A(﹣1，n)
(1)求反比例函数y＝的表达式.
(2)若两函数图象的另一交点为B，直接写出B的坐标.
暑假衔接教材期末暑假预习武汉出版社系列答案
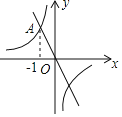
假期作业暑假成长乐园新疆青少年出版社系列答案科目：初中数学 来源： 题型：
【题目】“江畔”礼品店在十一月份从厂家购进甲、乙两种不同礼品．购进甲种礼品共花费1500元，购进乙种礼品共花费1050元，购进甲种礼品数量是购进乙种礼品数量的2倍，且购进一件乙种礼品比购进一件甲种礼品多花20元．
（1）求购进一件甲种礼品、一件乙种礼品各需多少元；
（2）元旦前夕，礼品店决定再次购进甲、乙两种礼品共50个．恰逢该厂家对两种礼品的价格进行调整，一件甲种礼品价格比第一次购进时提高了30%，件乙种礼品价格比第次购进时降低了10元，如果此次购进甲、乙两种礼品的总费用不超过3100元，那么这家礼品店最多可购进多少件甲种礼品?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场要经营一种新上市的文具，进价为20元，试营销阶段发现：当销售单价是25元时，每天的销售量为250件，销售单价每上涨1元，每天的销售量就减少10件
（1）写出商场销售这种文具，每天所得的销售利润
（元）与销售单价
（元）之间的函数关系式；
（2）求销售单价为多少元时，该文具每天的销售利润最大；
（3）商场的营销部结合上述情况，提出了A、B两种营销方案
方案A：该文具的销售单价高于进价且不超过30元；
方案B：每天销售量不少于10件，且每件文具的利润至少为25元
请比较哪种方案的最大利润更高，并说明理由
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知
是关于
的函数，若其函数图象经过点
，则称点
为函数图象上的“郡点”，例如：
上存在“郡点”
．
（1）直线___________（填写直线解析式）上的每一个点都是“郡点”，双曲线
上的“郡点”是___________；
（2）若抛物线
上有“郡点”，且“郡点”
、
（点和点可以重合）的坐标为
、
，求
的最小值．
（3）若函数
的图象上存在唯一的一个“郡点”，且当
，
的最小值
，求的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】合肥某企业安排65名工人生产甲、乙两种产品，每人每天生产2件甲或1件乙，甲产品每件可获利15元．根据市场需求和生产经验，乙产品每天产量不少于5件，当每天生产5件时，每件可获利120元，每增加1件，当天平均每件利润减少2元．设每天安排x人生产乙产品．
(1)根据信息填表：
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | _______ | _________ | 15 |
乙 | x | x | __________ |
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元，求每件乙产品可获得的利润；
(3)该企业在不增加工人的情况下，增加生产丙产品，要求每天甲、丙两种产品的产量相等．已知每人每天可生产1件丙(每人每天只能生产一件产品)，丙产品每件可获利30元，求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值．
查看答案和解析>>
科目：初中数学 来源： 题型：
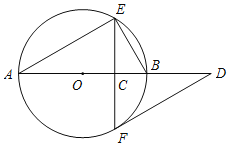
【题目】如图，AB是⊙O的直径，弦EF⊥AB于点C，过点F作⊙O的切线交AB的延长线于点D．
（1）已知∠A＝α，求∠D的大小（用含α的式子表示）；
（2）取BE的中点M，连接MF，请补全图形；若∠A＝30°，MF＝
，求⊙O的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB切⊙O与点A，BE切⊙O于点E，连接AO并延长交⊙O于点C，交BE的延长线于点D，连接EC，若AD＝8，tan∠DEC＝
，则CD＝_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市将实行居民生活用电阶梯电价方案，如下表，图中折线反映了每户居民每月电费
（元）与用电量
（度）间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
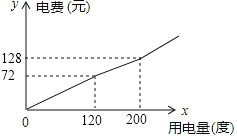
（1）小王家某月用电
度，需交电费___________元；
（2）求第二档电费（元）与用电量（度）之间的函数关系式；
（3）小王家某月用电
度，交纳电费
元，请你求出第三档每度电费比第二档每度电费多多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
