
����Ŀ�������ϡ���Ʒ����ʮһ�·ݴӳ��ҹ����ס������ֲ�ͬ��Ʒ������������Ʒ������1500Ԫ������������Ʒ������1050Ԫ������������Ʒ�����ǹ���������Ʒ������2�����ҹ���һ��������Ʒ�ȹ���һ��������Ʒ�20Ԫ��
��1����һ��������Ʒ��һ��������Ʒ�������Ԫ��
��2��Ԫ��ǰϦ����Ʒ������ٴι����ס���������Ʒ��50����ǡ��ó��Ҷ�������Ʒ�ļ۸���е�����һ��������Ʒ�۸�ȵ�һ�ι���ʱ�����30%����������Ʒ�۸�ȵڴι���ʱ������10Ԫ������˴ι����ס���������Ʒ���ܷ��ò�����3100Ԫ����ô�����Ʒ�����ɹ������ټ�������Ʒ?
���𰸡���1������һ��������Ʒ��Ҫ50Ԫ��һ��������Ʒ��70Ԫ����2�����ɹ���20��������Ʒ��
��������
��1���蹺��һ��������Ʒ��xԪ����һ��������Ʒ�裨x+20��Ԫ����������ã�![]() ,�ⷽ�̿ɵã�
,�ⷽ�̿ɵã�
��2���蹺����m��������![]() ������������ã�
������������ã�![]() ���ⲻ��ʽ�ɵ�.
���ⲻ��ʽ�ɵ�.
�⣺��1���蹺��һ��������Ʒ��xԪ����һ��������Ʒ�裨x+20��Ԫ��
��������ã�![]()
��ã�x=50
�����飬x=50��ԭ���̵Ľ⣬�ҷ������⣮
![]() =70Ԫ��
=70Ԫ��
�𣺹���һ��������Ʒ��Ҫ50Ԫ��һ��������Ʒ��70Ԫ��
��2���蹺����m��������![]() ����
����
��������ã�![]()
��ã�![]()
�����ɹ���20��������Ʒ��


 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ�Rt��ABC�Ķ�����ڸ���ϣ�����ƽ��ֱ������ϵ��A������Ϊ����4��1������B������Ϊ����1��1����
��1���Ƚ�Rt��ABC����ƽ��5����λ��������ƽ��1����λ��õ�Rt��A1B1C1������ͼ�л���ͼ��Rt��A1B1C1����д��A1�����ꣻ
��2����Rt��A1B1C1�Ƶ�A1˳ʱ����ת90���õ�Rt��A2B2C2������ͼ�л���ͼ��Rt��A2B2C2��������Rt��A1B1C1��������ת������C1��������·�̣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ��ڡ�O����CBG=��A��CDΪֱ����OC��AB�ཻ�ڵ�E������E��EF��BC������ΪF���ӳ�CD��GB���ӳ����ڵ�P������BD��
��1����֤��PG���O���У�
��2����![]() =
=![]() ����
����![]() ��ֵ��
��ֵ��
��3���ڣ�2���������£�����O�İ뾶Ϊ8��PD=OD����OE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������l1��y1��a(x+1)2+2��l2��y2����(x��2)2��1���ڵ�B(1����2)���ҷֱ���y�ύ�ڵ�D��E������B��x���ƽ���ߣ����������ڵ�A��C�������½��ۣ�
������xȡ��ֵ��y2���Ǹ�����
��l2����l1����ƽ��3����λ��������ƽ��3����λ�õ���
�۵���3��x��1ʱ������x������y1��y2��ֵ��������С��
���ı���AECDΪ�����Σ�
������ȷ����(����)
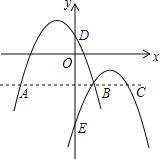
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ƕ��壺�Խ����ഹֱ���ı��ν��������ı��Σ�

��1����ͼ1�������ı���ABCD�ĶԽ���AC��BD����O����֤��AB2+CD2��AD2+BC2��
��2����ͼ2���ֱ���Rt��ACB��ֱ�DZ�AC��б��ABΪ��������������ACFG��������ABDE������BE��CG��GE��
����֤���ı���BCGE�Ǵ����ı��Σ�
����AC��4��AB��5����GE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ���ۺ���ʵ����С���ͬѧ�ѡ���������б�������˵�����ľ��롱��Ϊһ������������ƶ��˲��������������ÿ���ʱ���������б���������ʵ�ز���������������±���
��Ŀ | ���� | ||
���� | ����б�������˵�����ľ��� | ||
����ʾ��ͼ |
| ˵������������һ��б����AC��BC�ཻ�ڵ�C���ֱ������潻��A��B���㣬�ҵ�A��B��C��ͬһ��ֱƽ���ڣ� | |
�������� | ��A�Ķ��� | ��B�Ķ��� | AB�ij��� |
45�� | 30�� | 240�� | |
�� | �� | ||
�������С������ϱ��еIJ������ݣ���б�������˵�C��AB�ľ��룮�������ȷ��0.1�ף����ο����ݣ�![]() ��1.414��
��1.414��![]() ��1.732��
��1.732��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ѿ���Ϊһ��ʱ�У�ij���繺��ƽ̨��˫ʮһ��ȫ�콻������������2016�꽻��Ϊ500��Ԫ��2018�꽻��Ϊ720��Ԫ��
��1��2016����2018�ꡰ˫ʮһ���������ƽ���������Ƕ��٣�
��2��������ԭ���������ʣ��Լ���2019���ƽ̨��˫ʮһ���Ľ���ﵽ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
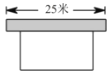
����Ŀ����ͼ��Ҫ��һ������������������������һ�߿�ǽ��ǽ��25�ף����������������Χ�ɣ�����ʵij�Ϊ40�ף���ҪΧ�ɵ������������Ϊ180ƽ���ף����������ij�������Ϊ�����ף�����ǽƽ�е�һ�߳�Ϊ![]() �ף�
�ף�
��1����գ����ú�![]() �Ĵ���ʽ��ʾ����һ�߳�Ϊ �ף�
�Ĵ���ʽ��ʾ����һ�߳�Ϊ �ף�
��2���г����̣����������Ľ⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y����2x��ͼ���뷴��������y��![]() ��ͼ���һ������ΪA(��1��n)
��ͼ���һ������ΪA(��1��n)
(1)��������y��![]() �ı���ʽ.
�ı���ʽ.
(2)��������ͼ�����һ����ΪB��ֱ��д��B������.
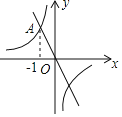
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com