
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпl1ЃКy1ЃНa(x+1)2+2гыl2ЃКy2ЃНЉ(xЉ2)2Љ1НЛгкЕуB(1ЃЌЉ2)ЃЌЧвЗжБ№гыyжсНЛгкЕуDЁЂEЃЎЙ§ЕуBзїxжсЕФЦНааЯпЃЌНЛХзЮяЯпгкЕуAЁЂCЃЌдђвдЯТНсТлЃК
ЂйЮоТлxШЁКЮжЕЃЌy2змЪЧИКЪ§ЃЛ
Ђкl2ПЩгЩl1ЯђгвЦНвЦ3ИіЕЅЮЛЃЌдйЯђЯТЦНвЦ3ИіЕЅЮЛЕУЕНЃЛ
ЂлЕБЉ3ЃМxЃМ1ЪБЃЌЫцзХxЕФдіДѓЃЌy1Љy2ЕФжЕЯШдіДѓКѓМѕаЁЃЛ
ЂмЫФБпаЮAECDЮЊе§ЗНаЮЃЎ
Цфжае§ШЗЕФЪЧ(ЁЁЁЁ)
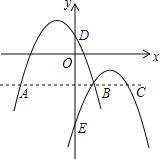
A.1ИіB.2ИіC.3ИіD.4Иі
ЁОД№АИЁПC
ЁОНтЮіЁП
ЂйгЩЗЧИКЪ§ЕФаджЪЃЌМДПЩжЄЕУy2ЃНЉ(xЉ2)2Љ1Ём-1ЃМ0ЃЌПЩЕУЮоТлxШЁКЮжЕЃЌy2змЪЧИКЪ§ЃЛ
ЂкгЩХзЮяЯпl1ЃКy1ЃНa(x+1)2+2гыl2ЃКy2ЃНЉ(xЉ2)2Љ1НЛгкЕуBЃЈ1ЃЌ-2ЃЉЃЌПЩЧѓЕУaЕФжЕЃЌШЛКѓгЩХзЮяЯпЕФЦНвЦЕФаджЪЃЌМДПЩЕУl2ПЩгЩl1ЯђгвЦНвЦ3ИіЕЅЮЛЃЌдйЯђЯТЦНвЦ3ИіЕЅЮЛЕУЕНЃЛ
ЂлгЩ y1- y2=-(x+1)2+2-[- (xЉ2)2Љ1]=-6x+6ЃЌПЩЕУЫцзХxЕФдіДѓЃЌy1- y2ЕФжЕМѕаЁЃЛ
ЂмЪзЯШЧѓЕУЕуAЃЌCЃЌDЃЌEЕФзјБъЃЌМДПЩжЄЕУAF=CF=DF=EFЃЌгжгЩACЁЭDEЃЌМДПЩжЄЕУЫФБпаЮAECDЮЊе§ЗНаЮЃЎ
НтЃКЂйЁпЃЈxЉ2ЃЉ2Ён0ЃЌ
ЁрЉЃЈxЉ2ЃЉ2Ём0ЃЌ
Ёрy2ЃНЉЃЈxЉ2ЃЉ2Љ1ЁмЉ1ЃМ0ЃЌ
ЁрЮоТлxШЁКЮжЕЃЌy2змЪЧИКЪ§ЃЛ
ЙЪЂйе§ШЗЃЛ
ЂкЁпХзЮяЯпl1ЃКy1ЃНaЃЈx+1ЃЉ2+2гыl2ЃКy2ЃНЉЃЈxЉ2ЃЉ2Љ1НЛгкЕуBЃЈ1ЃЌЉ2ЃЉЃЌ
ЁрЕБxЃН1ЪБЃЌyЃНЉ2ЃЌ
МДЉ2ЃНaЃЈ1+1ЃЉ2+2ЃЌ
НтЕУЃКaЃНЉ1ЃЛ
Ёрy1ЃНЉЃЈx+1ЃЉ2+2ЃЌ
Ёрl2ПЩгЩl1ЯђгвЦНвЦ3ИіЕЅЮЛЃЌдйЯђЯТЦНвЦ3ИіЕЅЮЛЕУЕНЃЛ
ЙЪЂке§ШЗЃЛ
ЂлЁпy1Љy2ЃНЉЃЈx+1ЃЉ2+2Љ[ЉЃЈxЉ2ЃЉ2Љ1]ЃНЉ6x+6ЃЌ
ЁрЫцзХxЕФдіДѓЃЌy1Љy2ЕФжЕМѕаЁЃЛ
ЙЪЂлДэЮѓЃЛ
ЂмЩшACгыDEНЛгкЕуFЃЌ
ЁпЕБyЃНЉ2ЪБЃЌЉЃЈx+1ЃЉ2+2ЃНЉ2ЃЌ
НтЕУЃКxЃНЉ3ЛђxЃН1ЃЌ
ЁрЕуAЃЈЉ3ЃЌЉ2ЃЉЃЌ
ЕБyЃНЉ2ЪБЃЌЉЃЈxЉ2ЃЉ2Љ1ЃНЉ2ЃЌ
НтЕУЃКxЃН3ЛђxЃН1ЃЌ
ЁрЕуCЃЈ3ЃЌЉ2ЃЉЃЌ
ЁрAFЃНCFЃН3ЃЌACЃН6ЃЌ
ЕБxЃН0ЪБЃЌy1ЃН1ЃЌy2ЃНЉ5ЃЌ
ЁрDEЃН6ЃЌDFЃНEFЃН3ЃЌ
ЁрЫФБпаЮAECDЮЊЦНааЫФБпаЮЃЌ
ЁрACЃНDEЃЌ
ЁрЫФБпаЮAECDЮЊОиаЮЃЌ
ЁпACЁЭDEЃЌ
ЁрЫФБпаЮAECDЮЊе§ЗНаЮЃЎ
ЙЪЂме§ШЗЃЎ
ЙЪбЁЃКCЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЁЯAOB=90ЁуЃЌABЁЮxжсЃЌOA=2ЃЌЫЋЧњЯп![]() ОЙ§ЕуAЃЎНЋЁїAOBШЦЕуAЫГЪБеыа§зЊЃЌЪЙЕуOЕФЖдгІЕуDТфдкxжсЕФИКАыжсЩЯЃЌШєABЕФЖдгІЯпЖЮACЧЁКУОЙ§ЕуOЃЎ
ОЙ§ЕуAЃЎНЋЁїAOBШЦЕуAЫГЪБеыа§зЊЃЌЪЙЕуOЕФЖдгІЕуDТфдкxжсЕФИКАыжсЩЯЃЌШєABЕФЖдгІЯпЖЮACЧЁКУОЙ§ЕуOЃЎ
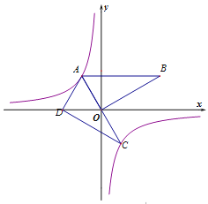
ЃЈ1ЃЉЧѓЕуAЕФзјБъКЭЫЋЧњЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉХаЖЯЕуCЪЧЗёдкЫЋЧњЯпЩЯЃЌВЂЫЕУїРэгЩ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЫФБпаЮ
жаЃЌЫФБпаЮ![]() ЪЧОиаЮЃЌ
ЪЧОиаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЖЏЕу
ЃЌЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌбиЩфЯп
ГіЗЂЃЌбиЩфЯп![]() ЗНЯђвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЛЭЌЪБЃЌЖЏЕу
ЗНЯђвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЛЭЌЪБЃЌЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌби
ГіЗЂЃЌби![]() жсе§АыжсЗНЯђвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЩшЕу
жсе§АыжсЗНЯђвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЩшЕу![]() ЁЂЕу
ЁЂЕу![]() ЕФдЫЖЏЪБМфЮЊ
ЕФдЫЖЏЪБМфЮЊ![]()
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓОЙ§Еу
ЪБЃЌЧѓОЙ§Еу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§ЕуЕФХзЮяЯпЕФНтЮіЪНЃЛ
Ш§ЕуЕФХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉЕБЯпЖЮ![]() гыЯпЖЮ
гыЯпЖЮ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЧв
ЃЌЧв![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ4ЃЉСЌНг![]() ЃЌЕБЕу
ЃЌЕБЕу![]() ЃЌ
ЃЌ![]() дкдЫЖЏЙ§ГЬжаЃЌМЧЁї
дкдЫЖЏЙ§ГЬжаЃЌМЧЁї![]() гыОиаЮ
гыОиаЮ![]() жиЕўВПЗжЕФУцЛ§ЮЊ
жиЕўВПЗжЕФУцЛ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪН
ЕФКЏЪ§ЙиЯЕЪН
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
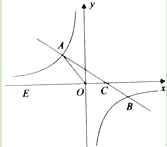
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕx0yжаЃЌвЛДЮКЏЪ§y=kx+bЃЈkЁй0ЃЉЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЃЈmЁй0ЃЉЕФЭМЯѓНЛгкЖўЁЂЫФЯѓЯоФкЕФAЁЂBСНЕуЃЌгыxжсНЛгкCЕуЃЌЕуBЕФзјБъЮЊЃЈ6ЃЌnЃЉЃЎЯпЖЮOA=5ЃЌEЮЊxжсЩЯвЛЕуЃЌЧвsinЁЯAOE=
ЃЈmЁй0ЃЉЕФЭМЯѓНЛгкЖўЁЂЫФЯѓЯоФкЕФAЁЂBСНЕуЃЌгыxжсНЛгкCЕуЃЌЕуBЕФзјБъЮЊЃЈ6ЃЌnЃЉЃЎЯпЖЮOA=5ЃЌEЮЊxжсЩЯвЛЕуЃЌЧвsinЁЯAOE=![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓИУЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЁїAOCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
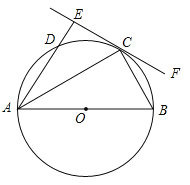
ЁОЬтФПЁПШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌCЁЂDЮЊЁбOЩЯЕФСНЕуЃЌЁЯBAC=ЁЯDACЃЌЙ§ЕуCзіжБЯпEFЁЭADЃЌНЛADЕФбгГЄЯпгкЕуEЃЌСЌНгBCЃЎ
ЃЈ1ЃЉЧѓжЄЃКEFЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєDE=1ЃЌBC=2ЃЌЧѓСгЛЁ![]() ЕФГЄlЃЎ
ЕФГЄlЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
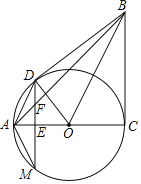
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌвдACЮЊжБОЖзїЁбOЃЌЕуDдкЁбOЩЯЃЌBDЃНBCЃЌDEЁЭACЃЌДЙзуЮЊЕуEЃЌDEгыЁбOКЭABЗжБ№НЛгкЕуMЁЂFЃЎСЌНгBOЁЂDOЁЂAMЃЎ
(1)жЄУїЃКBDЪЧЁбOЕФЧаЯпЃЛ
(2)ШєtanЁЯAMDЃН![]() ЃЌADЃН2
ЃЌADЃН2![]() ЃЌЧѓЁбOЕФАыОЖГЄЃЛ
ЃЌЧѓЁбOЕФАыОЖГЄЃЛ
(3)дк(2)ЕФЬѕМўЯТЃЌЧѓDFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАНХЯЁБРёЦЗЕъдкЪЎвЛдТЗнДгГЇМвЙКНјМзЁЂввСНжжВЛЭЌРёЦЗЃЎЙКНјМзжжРёЦЗЙВЛЈЗб1500дЊЃЌЙКНјввжжРёЦЗЙВЛЈЗб1050дЊЃЌЙКНјМзжжРёЦЗЪ§СПЪЧЙКНјввжжРёЦЗЪ§СПЕФ2БЖЃЌЧвЙКНјвЛМўввжжРёЦЗБШЙКНјвЛМўМзжжРёЦЗЖрЛЈ20дЊЃЎ
ЃЈ1ЃЉЧѓЙКНјвЛМўМзжжРёЦЗЁЂвЛМўввжжРёЦЗИїашЖрЩйдЊЃЛ
ЃЈ2ЃЉдЊЕЉЧАЯІЃЌРёЦЗЕъОіЖЈдйДЮЙКНјМзЁЂввСНжжРёЦЗЙВ50ИіЃЎЧЁЗъИУГЇМвЖдСНжжРёЦЗЕФМлИёНјааЕїећЃЌвЛМўМзжжРёЦЗМлИёБШЕквЛДЮЙКНјЪБЬсИпСЫ30%ЃЌМўввжжРёЦЗМлИёБШЕкДЮЙКНјЪБНЕЕЭСЫ10дЊЃЌШчЙћДЫДЮЙКНјМзЁЂввСНжжРёЦЗЕФзмЗбгУВЛГЌЙ§3100дЊЃЌФЧУДетМвРёЦЗЕъзюЖрПЩЙКНјЖрЩйМўМзжжРёЦЗ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
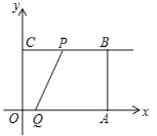
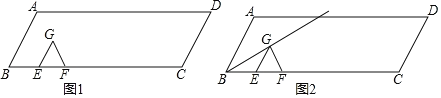
ЁОЬтФПЁПШчЭМ1ЃЌдкABCDжаЃЌAB=2ЃЌBC=6ЃЌЁЯD=60ЁуЃЌЕуEДгBЕуГіЗЂбизХЯпЖЮBCУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђCдЫЖЏЃЌЭЌЪБЕуFДгBЕуГіЗЂбизХЩфЯпBCУПУы2ЕЅЮЛГЄЖШЕФЫйЖШЯђCдЫЖЏЃЌвдEFЮЊБпдкжБЯпBCЩЯЗНзїЕШБпЁїEFGЃЌЩшЕуEЁЂFЕФдЫЖЏЪБМфЮЊtУыЃЌЦфжа0ЃМtЁм4ЃЎ
ЃЈ1ЃЉЕБt=ЁЁЁЁЁЁЁЁУыЪБЃЌЕуGТфдкЯпЖЮADЩЯЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгBGЃЌЪдЫЕУїЃКЮоТлtЮЊКЮжЕЃЌBGЪМжеЦНЗжЁЯABCЃЛ
ЃЈ3ЃЉЧѓЁїEFGгыABCDжиЕўВПЗжУцЛ§yгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌЕБtШЁКЮжЕЪБЃЌyгазюДѓжЕЃПВЂЧѓГіyЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЪЧЙигк
ЪЧЙигк![]() ЕФКЏЪ§ЃЌШєЦфКЏЪ§ЭМЯѓОЙ§Еу
ЕФКЏЪ§ЃЌШєЦфКЏЪ§ЭМЯѓОЙ§Еу![]() ЃЌдђГЦЕу
ЃЌдђГЦЕу![]() ЮЊКЏЪ§ЭМЯѓЩЯЕФЁАПЄЕуЁБЃЌР§ШчЃК
ЮЊКЏЪ§ЭМЯѓЩЯЕФЁАПЄЕуЁБЃЌР§ШчЃК![]() ЩЯДцдкЁАПЄЕуЁБ
ЩЯДцдкЁАПЄЕуЁБ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉжБЯп___________ЃЈЬюаДжБЯпНтЮіЪНЃЉЩЯЕФУПвЛИіЕуЖМЪЧЁАПЄЕуЁБЃЌЫЋЧњЯп![]() ЩЯЕФЁАПЄЕуЁБЪЧ___________ЃЛ
ЩЯЕФЁАПЄЕуЁБЪЧ___________ЃЛ
ЃЈ2ЃЉШєХзЮяЯп![]() ЩЯгаЁАПЄЕуЁБЃЌЧвЁАПЄЕуЁБ
ЩЯгаЁАПЄЕуЁБЃЌЧвЁАПЄЕуЁБ![]() ЁЂ
ЁЂ![]() ЃЈЕу
ЃЈЕу![]() КЭЕу
КЭЕу![]() ПЩвджиКЯЃЉЕФзјБъЮЊ
ПЩвджиКЯЃЉЕФзјБъЮЊ![]() ЁЂ
ЁЂ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
ЃЈ3ЃЉШєКЏЪ§![]() ЕФЭМЯѓЩЯДцдкЮЈвЛЕФвЛИіЁАПЄЕуЁБЃЌЧвЕБ
ЕФЭМЯѓЩЯДцдкЮЈвЛЕФвЛИіЁАПЄЕуЁБЃЌЧвЕБ![]() ЃЌ
ЃЌ![]() ЕФзюаЁжЕ
ЕФзюаЁжЕ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com