
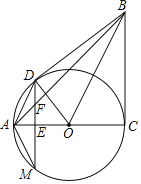
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O,点D在⊙O上,BD=BC,DE⊥AC,垂足为点E,DE与⊙O和AB分别交于点M、F.连接BO、DO、AM.
(1)证明:BD是⊙O的切线;
(2)若tan∠AMD=![]() ,AD=2
,AD=2![]() ,求⊙O的半径长;
,求⊙O的半径长;
(3)在(2)的条件下,求DF的长.
【答案】(1)见解析;(2)圆的半径为5;(3)DF=2
【解析】
(1)证明△BDO≌△BCO(SSS),则∠BDO=∠ABC=90°,即可求解;
(2)在Rt△ADC中,tan∠ACD=tan∠AMD=![]() ,则AD=2
,则AD=2![]() ,CD=4
,CD=4![]() ,即可求解;
,即可求解;
(3)证明△DAE∽△BOC,则![]() ,即
,即![]() ,解得:BC=10,则FE=AE=2,DF=DE-EF=2.
,解得:BC=10,则FE=AE=2,DF=DE-EF=2.
解:(1)在△BDO和△BCO中,
BD=BC,OD=OC,BO=BO,
故△BDO≌△BCO(SSS),
∴∠BDO=∠ABC=90°,
∴BD是⊙O的切线;
(2)连接CD,则∠AMD=∠ACD,
AB是直径,故∠ADC=90°,
在Rt△ADC中,tan∠ACD=tan∠AMD=![]() ,
,
∵AD=2![]() ,
,
∴CD=4![]() ,
,
∴AC=![]() ,
,
故圆的半径为5;
(3)在Rt△ADC中,DE⊥AC,
则DE=![]() ,则AE=2,
,则AE=2,
由(1)知△BDO≌△BCO,
∴∠BOC=∠BOD=![]() ∠DOC,
∠DOC,
∵∠DAE=![]() ∠DOC,
∠DOC,
∴∠DAE=∠BOC,
∵ED⊥AC,
∴∠AED=∠OCB=90°,
∴△DAE∽△BOC,
∴![]() ,即
,即![]() ,解得:BC=10,
,解得:BC=10,
∴∠BAC=∠ABC=45°,
∴∠FAE=∠AFE=45°,
∴FE=AE=2,
∴DF=DE﹣EF=2.


科目:初中数学 来源: 题型:
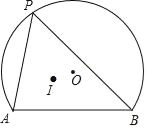
【题目】如图,AB为弓形AB的弦,AB=2![]() ,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为_____.
,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 | 乙 | 丙 | |
单价(元/棵) | 14 | 16 | 28 |
合理用地(m2/棵) | 0.4 | 1 | 0.4 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
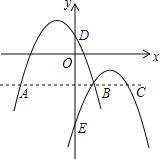
【题目】如图,抛物线l1:y1=a(x+1)2+2与l2:y2=﹣(x﹣2)2﹣1交于点B(1,﹣2),且分别与y轴交于点D、E.过点B作x轴的平行线,交抛物线于点A、C,则以下结论:
①无论x取何值,y2总是负数;
②l2可由l1向右平移3个单位,再向下平移3个单位得到;
③当﹣3<x<1时,随着x的增大,y1﹣y2的值先增大后减小;
④四边形AECD为正方形.
其中正确的是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学“综合与实践”小组的同学把“测量大桥斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下表.
项目 | 内容 | ||
课题 | 测量斜拉索顶端到桥面的距离 | ||
测量示意图 |
| 说明:大桥两侧一组斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内. | |
测量数据 | ∠A的度数 | ∠B的度数 | AB的长度 |
45° | 30° | 240米 | |
… | … | ||
请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离.(结果精确到0.1米)(参考数据:![]() =1.414,
=1.414,![]() =1.732)
=1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为60m2的三个项目的任务,三个项目的面积比例和每人每分钟完成各所示:项目的工作量如图:
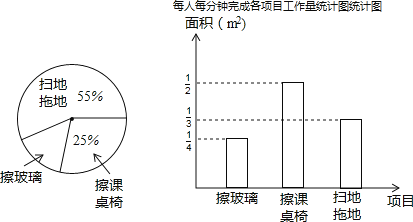
(1)从统计图中可知:擦玻璃的面积占总面积的百分比为 ,每人每分钟擦课桌椅 m2;
(2)扫地拖地的面积是 m2;
(3)他们一起完成扫地和拖地任务后,把这13人分成两组,一组去擦玻璃,一组去擦课桌椅,如果你是卫生委员,该如何分配这两组的人数,才能最快地完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于第一、三象限内的
的图象相交于第一、三象限内的![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)直接写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最大,求
最大,求![]() 的最大值及点
的最大值及点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com