
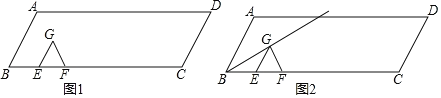
【题目】如图1,在ABCD中,AB=2,BC=6,∠D=60°,点E从B点出发沿着线段BC每秒1个单位长度的速度向C运动,同时点F从B点出发沿着射线BC每秒2单位长度的速度向C运动,以EF为边在直线BC上方作等边△EFG,设点E、F的运动时间为t秒,其中0<t≤4.
(1)当t= 秒时,点G落在线段AD上;
(2)如图2,连接BG,试说明:无论t为何值,BG始终平分∠ABC;
(3)求△EFG与ABCD重叠部分面积y与t之间的函数关系式,当t取何值时,y有最大值?并求出y的最大值.
【答案】(1)2;(2)理由见解析;(3)y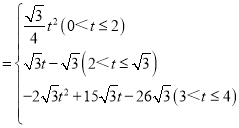 ;当t
;当t![]() 时,y的最大值为:
时,y的最大值为:![]() .
.
【解析】
(1)设等边三角形的边长为a,等边△EFG的边长为t,当点G落在线段AD上,即等边△EFG的高等于ABCD的高.
(2)如图1,△GEF为边长为t的等边三角形,BE=t=EF=GE,则∠GBE=∠EGB,即可求解;
(3)①当0<t≤2时,重叠部分为△EFG,y=S△EFG=![]() t2;②当2<t≤3时,如图2,重叠部分为四边形HMEF,y=S△EFG-S△HMG=
t2;②当2<t≤3时,如图2,重叠部分为四边形HMEF,y=S△EFG-S△HMG=![]() t2-
t2-![]() (t-2)2=
(t-2)2=![]() t-
t-![]() ;③当3<t≤4时,y=S△GEF-(S△GHM+S△MND+S△NCF),即可求解.
;③当3<t≤4时,y=S△GEF-(S△GHM+S△MND+S△NCF),即可求解.
(1)设等边三角形的边长为a,则面积为:![]() a2,
a2,
ABCD的高为ABsin∠ABC=ABsin∠D![]()
等边△EFG的边长为t,则高为![]() t
t
当点G落在线段AD上,![]() t
t![]() ,解得:t=2.
,解得:t=2.
故答案为:2;
(2)如图1,△GEF为边长为t的等边三角形,
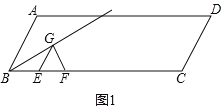
BE=t=EF=GE,则∠GBE=∠EGB,
∠GBE=60°=2∠GBE=2∠EGB,
故∠GBE=30°,而∠ABC=∠D=60°,
∠ABG=∠GBE=30°,
∴BG始终平分∠ABC;
(3)△EFG始终为边长为t的等边三角形,则S△EFG![]() t2,
t2,
①当0<t≤2时,重叠部分为△EFG,
y=S△EFG![]() t2;
t2;
此时,当t=2时,y最大值为![]() ;
;
②当2<t≤3时,如图2,重叠部分为四边形HMEF,
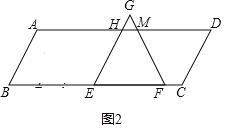
则△HMG为边长为(t﹣2)的等边三角形,
则y=S△EFG﹣S△HMG![]() t2
t2![]() (t﹣2)2
(t﹣2)2![]() t
t![]() ;
;
当t=3时,y的最大值为:2![]() ;
;
③当3<t≤4时,
△GMH、△MND、△FCN均为等边三角形,
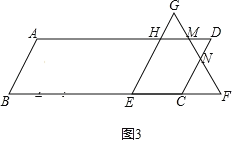
△GMH的边长HG=GE﹣HE=GE﹣AB=t﹣2,
△FCN的边长FC=EF﹣EC=t﹣(6﹣t)=2t﹣6,
△MND的边长MN=MF﹣NF=2﹣(2t﹣6)=8﹣2t,
y=S△GEF﹣(S△GHM+S△MND+S△NCF)![]() [t2﹣(t﹣2)2﹣(2t﹣6)2﹣(8﹣2t)2]=﹣2
[t2﹣(t﹣2)2﹣(2t﹣6)2﹣(8﹣2t)2]=﹣2![]() t2+15
t2+15![]() t﹣26
t﹣26![]() ,
,
当t![]() 时,y的最大值为:
时,y的最大值为:![]() ;
;
综上,y ;
;
当t![]() 时,y的最大值为:
时,y的最大值为:![]() .
.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过圆外一点作这个圆的两条切线”的尺规作图过程.
已知:⊙O及⊙O外一点P.
求作:直线PA和直线PB,使PA切⊙O于点A,PB切⊙O于点B.
作法:如图,
①连接OP,分别以点O和点P为圆心,大于![]() OP的同样长为半径作弧,两弧分别交于点M,N;
OP的同样长为半径作弧,两弧分别交于点M,N;
②连接MN,交OP于点Q,再以点Q为圆心,OQ的长为半径作弧,交⊙O于点A和点B;
③作直线PA和直线PB.
所以直线PA和PB就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
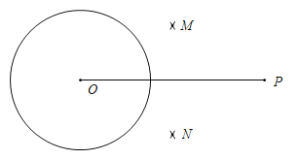
(2)完成下面的证明.
证明:∵OP是⊙Q的直径,
∴ ∠OAP=∠OBP=________°( )(填推理的依据).
∴PA⊥OA,PB⊥OB.
∵OA,OB为⊙O的半径,
∴PA,PB是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线l1:y1=a(x+1)2+2与l2:y2=﹣(x﹣2)2﹣1交于点B(1,﹣2),且分别与y轴交于点D、E.过点B作x轴的平行线,交抛物线于点A、C,则以下结论:
①无论x取何值,y2总是负数;
②l2可由l1向右平移3个单位,再向下平移3个单位得到;
③当﹣3<x<1时,随着x的增大,y1﹣y2的值先增大后减小;
④四边形AECD为正方形.
其中正确的是( )
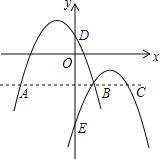
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学“综合与实践”小组的同学把“测量大桥斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下表.
项目 | 内容 | ||
课题 | 测量斜拉索顶端到桥面的距离 | ||
测量示意图 |
| 说明:大桥两侧一组斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内. | |
测量数据 | ∠A的度数 | ∠B的度数 | AB的长度 |
45° | 30° | 240米 | |
… | … | ||
请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离.(结果精确到0.1米)(参考数据:![]() =1.414,
=1.414,![]() =1.732)
=1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网购已经成为一种时尚,某网络购物平台“双十一”全天交易额逐年增长,2016年交易额为500亿元,2018年交易额为720亿元。
(1)2016年至2018年“双十一”交易额的年平均增长率是多少?
(2)若保持原来的增长率,试计算2019年该平台“双十一”的交易额将达到多少亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为60m2的三个项目的任务,三个项目的面积比例和每人每分钟完成各所示:项目的工作量如图:
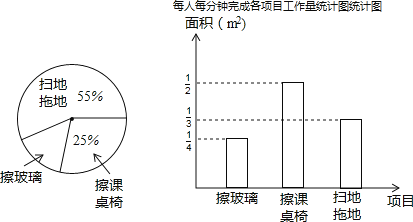
(1)从统计图中可知:擦玻璃的面积占总面积的百分比为 ,每人每分钟擦课桌椅 m2;
(2)扫地拖地的面积是 m2;
(3)他们一起完成扫地和拖地任务后,把这13人分成两组,一组去擦玻璃,一组去擦课桌椅,如果你是卫生委员,该如何分配这两组的人数,才能最快地完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
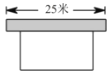
【题目】如图,要建一个长方形养鸡场,养鸡场的一边靠墙(墙长25米),另三边用竹篱笆围成,竹篱笆的长为40米,若要围成的养鸡场的面积为180平方米,求养鸡场的长、宽各为多少米,设与墙平行的一边长为![]() 米.
米.
(1)填空:(用含![]() 的代数式表示)另一边长为 米;
的代数式表示)另一边长为 米;
(2)列出方程,并求出问题的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
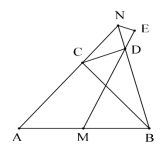
【题目】如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20![]() ,MD=14
,MD=14![]() ,则 NE 的长为___.
,则 NE 的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次三项式﹣x2+2x+3.
(1)关于x的一元二次方程﹣x2+2x+3=﹣mx2+mx+2(m为整数)的根为有理数,求m的值;
(2)在平面直角坐标系中,直线y=﹣2x+n分别交x,y轴于点A,B,若函数y=﹣x2+2|x|+3的图象与线段AB只有一个交点,求n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com