
ĄūĖâÄŋĄŋŌŅÖŠĢšČįÍžËųĘūĢŽÔÚÆ―ÃæÖą―ĮŨøąęÏĩ![]() ÖÐĢŽËÄąßÐÎ
ÖÐĢŽËÄąßÐÎ![]() ĘĮūØÐÎĢŽ
ĘĮūØÐÎĢŽ![]() ĢŽ
ĢŽ![]() ĢŽķŊĩã
ĢŽķŊĩã![]() īÓĩã
īÓĩã![]() ģö·ĒĢŽŅØÉäÏß
ģö·ĒĢŽŅØÉäÏß![]() ·―ÏōŌÔÃŋÃë2ļöĩĨÎŧģĪķČĩÄËŲķČÔËķŊĢŧÍŽĘąĢŽķŊĩã
·―ÏōŌÔÃŋÃë2ļöĩĨÎŧģĪķČĩÄËŲķČÔËķŊĢŧÍŽĘąĢŽķŊĩã![]() īÓĩã
īÓĩã![]() ģö·ĒĢŽŅØ
ģö·ĒĢŽŅØ![]() ÖáÕý°ëÖá·―ÏōŌÔÃŋÃë1ļöĩĨÎŧģĪķČĩÄËŲķČÔËķŊĢŽÉčĩã
ÖáÕý°ëÖá·―ÏōŌÔÃŋÃë1ļöĩĨÎŧģĪķČĩÄËŲķČÔËķŊĢŽÉčĩã![]() ĄĒĩã
ĄĒĩã![]() ĩÄÔËķŊĘąžäΊ
ĩÄÔËķŊĘąžäΊ![]()
ĢĻ1ĢĐĩą![]() ĘąĢŽĮóūđýĩã
ĘąĢŽĮóūđýĩã![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ČýĩãĩÄÅŨÎïÏßĩÄ―âÎöĘ―Ģŧ
ČýĩãĩÄÅŨÎïÏßĩÄ―âÎöĘ―Ģŧ
ĢĻ2ĢĐĩą![]() ĘąĢŽĮó
ĘąĢŽĮó![]() ĩÄÖĩĢŧ
ĩÄÖĩĢŧ
ĢĻ3ĢĐĩąÏßķÎ![]() ÓëÏßķÎ
ÓëÏßķÎ![]() Ïā―ŧÓÚĩã
Ïā―ŧÓÚĩã![]() ĢŽĮŌ
ĢŽĮŌ![]() ĘąĢŽĮó
ĘąĢŽĮó![]() ĩÄÖĩĢŧ
ĩÄÖĩĢŧ
ĢĻ4ĢĐÁŽ―Ó![]() ĢŽĩąĩã
ĢŽĩąĩã![]() ĢŽ
ĢŽ![]() ÔÚÔËķŊđýģĖÖÐĢŽžĮĄũ
ÔÚÔËķŊđýģĖÖÐĢŽžĮĄũ![]() ÓëūØÐÎ
ÓëūØÐÎ![]() ÖØĩþēŋ·ÖĩÄÃæŧýΊ
ÖØĩþēŋ·ÖĩÄÃæŧýΊ![]() ĢŽĮó
ĢŽĮó![]() Óë
Óë![]() ĩÄšŊĘýđØÏĩĘ―
ĩÄšŊĘýđØÏĩĘ―
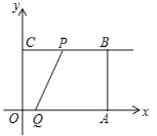
Ąūīð°ļĄŋĢĻ1ĢĐy=Đ![]() x2+3xĢŧĢĻ2ĢĐ
x2+3xĢŧĢĻ2ĢĐ![]() ĢŧĢĻ3ĢĐtΊ3sĢŧĢĻ4ĢĐS=
ĢŧĢĻ3ĢĐtΊ3sĢŧĢĻ4ĢĐS=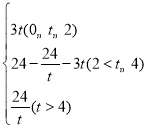
Ąū―âÎöĄŋ
ĢĻ1ĢĐŋÉĮóĩÃPĩãŨøąęĢŽÓÉOĄĒPĄĒAĩÄŨøąęĢŽĀûÓÃīýķĻÏĩĘý·ĻŋÉĮóĩÃÅŨÎïÏß―âÎöĘ―Ģŧ
ĢĻ2ĢĐĩątĢ―2sĘąĢŽŋÉÖŠPÓëĩãBÖØšÏĢŽÔÚRtĄũABQÖÐŋÉĮóĩÃtanĄÏQPAĩÄÖĩĢŧ
ĢĻ3ĢĐÓÃtŋÉąíĘūģöBPšÍAQĩÄģĪĢŽÓÉĄũPBMĄŨĄũQAMŋÉĩÃĩ―đØÓÚtĩÄ·―ģĖĢŽŋÉĮóĩÃtĩÄÖĩĢŧ
ĢĻ4ĢĐĩąĩãQÔÚÏßķÎOAÉÏĘąĢŽSĢ―SĄũCPQĢŧĩąĩãQÔÚÏßķÎOAÉÏĢŽĮŌĩãPÔÚÏßķÎCBĩÄŅÓģĪÏßÉÏĘąĢŽÓÉÏāËÆČý―ĮÐÎĩÄÐÔÖĘŋÉÓÃtąíĘūģöAMĩÄģĪĢŽÓÉSĢ―SËÄąßÐÎBCQMĢ―SūØÐÎOABCSĄũCOQSĄũAMQĢŽŋÉĮóĩÃSÓëtĩÄđØÏĩĘ―ĢŧĩąĩãQÔÚOAĩÄŅÓģĪÏßÉÏĘąĢŽÉčCQ―ŧABÓÚĩãMĢŽĀûÓÃĄũAQMĄŨĄũBCMŋÉÓÃtąíĘūģöAMĢŽīÓķøŋÉąíĘūģöBMĢŽSĢ―SĄũCBMĢŽŋÉĮóĩÃīð°ļĢŪ
―âĢšĢĻ1ĢĐĩąt=1sĘąĢŽÔōCP=2ĢŽ
ĄßOC=3ĢŽËÄąßÐÎOABCĘĮūØÐÎĢŽ
ĄāPĢĻ2ĢŽ3ĢĐĢŽĮŌAĢĻ4ĢŽ0ĢĐĢŽ
ĄßÅŨÎïÏßđýÔĩãOĢŽ
ĄāŋÉÉčÅŨÎïÏß―âÎöĘ―ÎŠy=ax2+bxĢŽ
Ąā![]() ĢŽ―âĩÃ
ĢŽ―âĩÃ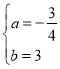 ĢŽ
ĢŽ
ĄāđýOĄĒPĄĒAČýĩãĩÄÅŨÎïÏßĩÄ―âÎöĘ―ÎŠy=Đ![]() x2+3xĢŧ
x2+3xĢŧ
ĢĻ2ĢĐĩąt=2sĘąĢŽÔōCP=2ĄÁ2=4=BCĢŽžīĩãPÓëĩãBÖØšÏĢŽOQ=2ĢŽČįÍž1ĢŽ
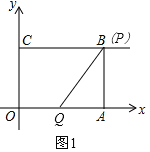
ĄāAQ=OAĐOQ=4Đ2=2ĢŽĮŌAP=OC=3ĢŽ
ĄātanĄÏQPA=![]() =
=![]() Ģŧ
Ģŧ
ĢĻ3ĢĐĩąÏßķÎPQÓëÏßķÎABÏā―ŧÓÚĩãMĢŽÔōŋÉÖŠĩãQÔÚÏßķÎOAÉÏĢŽĩãPÔÚÏßķÎCBĩÄŅÓģĪÏßÉÏĢŽČįÍž2ĢŽ
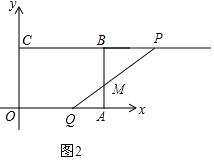
ÔōCP=2tĢŽOQ=tĢŽ
ĄāBP=PCĐCB=2tĐ4ĢŽAQ=OAĐOQ=4ĐtĢŽ
ĄßPCĄÎOAĢŽ
ĄāĄũPBMĄŨĄũQAMĢŽ
Ąā![]() ĢŽĮŌBM=2AMĢŽ
ĢŽĮŌBM=2AMĢŽ
Ąā![]() =2ĢŽ―âĩÃt=3ĢŽ
=2ĢŽ―âĩÃt=3ĢŽ
ĄāĩąÏßķÎPQÓëÏßķÎABÏā―ŧÓÚĩãMĢŽĮŌBM=2AMĘąĢŽtΊ3sĢŧ
ĢĻ4ĢĐĩą0ĄÜtĄÜ2ĘąĢŽČįÍž3ĢŽ

ÓÉĖâŌâŋÉÖŠCP=2tĢŽ
ĄāS=SĄũPCQ=![]() ĄÁ2tĄÁ3=3tĢŧ
ĄÁ2tĄÁ3=3tĢŧ
ĩą2ĢžtĄÜ4ĘąĢŽÉčPQ―ŧABÓÚĩãMĢŽČįÍž4ĢŽ
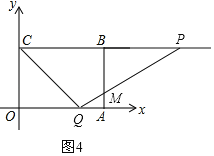
ÓÉĖâŌâŋÉÖŠPC=2tĢŽOQ=tĢŽÔōBP=2tĐ4ĢŽAQ=4ĐtĢŽ
ÍŽĢĻ3ĢĐŋÉĩÃ![]() =
=![]() ĢŽ
ĢŽ
ĄāBM=![]() AMĢŽ
AMĢŽ
Ąā3ĐAM=![]() AMĢŽ―âĩÃAM=
AMĢŽ―âĩÃAM=![]() ĢŽ
ĢŽ
ĄāS=SËÄąßÐÎBCQM=SūØÐÎOABCĐSĄũCOQĐSĄũAMQ=3ĄÁ4Đ![]() ĄÁtĄÁ3Đ
ĄÁtĄÁ3Đ![]() ĄÁĢĻ4ĐtĢĐĄÁ
ĄÁĢĻ4ĐtĢĐĄÁ![]() =24Đ
=24Đ![]() Đ3tĢŧ
Đ3tĢŧ
ĩątĢū4ĘąĢŽÉčCQÓëAB―ŧÓÚĩãMĢŽČįÍž5ĢŽ
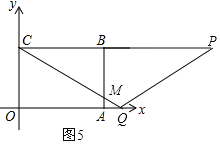
ÓÉĖâŌâŋÉÖŠOQ=tĢŽAQ=tĐ4ĢŽ
ĄßABĄÎOCĢŽ
Ąā![]() ĢŽžī
ĢŽžī![]() =
=![]() ĢŽ―âĩÃAM=
ĢŽ―âĩÃAM=![]() ĢŽ
ĢŽ
ĄāBM=3Đ![]() ĢŽ
ĢŽ
ĄāS=SĄũBCM=![]() ĄÁ4ĄÁ
ĄÁ4ĄÁ![]() Ģŧ
Ģŧ
ŨÛÉÏŋÉÖŠS=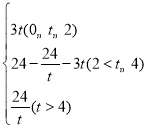 ĢŪ
ĢŪ


 ĖėĖėÏōÉÏŌŧąūšÃūíÏĩÁÐīð°ļ
ĖėĖėÏōÉÏŌŧąūšÃūíÏĩÁÐīð°ļ ÐĄŅ§Éú10·ÖÖÓÓĶÓÃĖâÏĩÁÐīð°ļ
ÐĄŅ§Éú10·ÖÖÓÓĶÓÃĖâÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
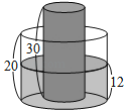
ĄūĖâÄŋĄŋČįÍžĢŽÓÐŌŧÄÚēŋŨ°ÓÐËŪĩÄÖąÔēÖųÐÎËŪÍ°ĢŽÍ°ļß![]() ĢŧÁíÓÐŌŧÖąÔēÖųÐÎĩÄĘĩÐÄĖúÖųĢŽÖųļß
ĢŧÁíÓÐŌŧÖąÔēÖųÐÎĩÄĘĩÐÄĖúÖųĢŽÖųļß![]() ĢŽÖąÁĒ·ÅÖÃÓÚËŪÍ°ĩŨÃæÉÏĢŽËŪÍ°ÄÚĩÄËŪÃæļßķČΊ
ĢŽÖąÁĒ·ÅÖÃÓÚËŪÍ°ĩŨÃæÉÏĢŽËŪÍ°ÄÚĩÄËŪÃæļßķČΊ![]() ĢŽĮŌËŪÍ°ÓëĖúÖųĩÄĩŨÃæ°ëūķąČΊ
ĢŽĮŌËŪÍ°ÓëĖúÖųĩÄĩŨÃæ°ëūķąČΊ![]() ĢŪ―ņÐĄÏÍ―ŦĖúÖųŌÆÖÁËŪÍ°ÍâēŋĢŽđýģĖÖÐËŪÍ°ÄÚĩÄËŪÁŋÎīļÄąäĢŽČôēŧžÆËŪÍ°šņķČĢŽÔōËŪÍ°ÄÚĩÄËŪÃæļßķČąäΊĢĻ ĢĐ
ĢŪ―ņÐĄÏÍ―ŦĖúÖųŌÆÖÁËŪÍ°ÍâēŋĢŽđýģĖÖÐËŪÍ°ÄÚĩÄËŪÁŋÎīļÄąäĢŽČôēŧžÆËŪÍ°šņķČĢŽÔōËŪÍ°ÄÚĩÄËŪÃæļßķČąäΊĢĻ ĢĐ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽ·―ļņÖ―ÖÐĩÄÃŋļöÐĄ·―ļņķžĘĮąßģĪΊ1ļöĩĨÎŧĩÄÕý·―ÐÎĢŪRtĄũABCĩÄķĨĩãūųÔÚļņĩãÉÏĢŽ―ĻÁĒÆ―ÃæÖą―ĮŨøąęÏĩšóĢŽĩãAĩÄŨøąęΊĢĻĐ4ĢŽ1ĢĐĢŽĩãBĩÄŨøąęΊĢĻĐ1ĢŽ1ĢĐĢŪ
ĢĻ1ĢĐÏČ―ŦRtĄũABCÏōÓŌÆ―ŌÆ5ļöĩĨÎŧĢŽÔŲÏōÏÂÆ―ŌÆ1ļöĩĨÎŧšóĩÃĩ―RtĄũA1B1C1ĢŪĘÔÔÚÍžÖÐŧģöÍžÐÎRtĄũA1B1C1ĢŽēĒÐīģöA1ĩÄŨøąęĢŧ
ĢĻ2ĢĐ―ŦRtĄũA1B1C1ČÆĩãA1ËģĘąÕëÐýŨŠ90ĄãšóĩÃĩ―RtĄũA2B2C2ĢŽĘÔÔÚÍžÖÐŧģöÍžÐÎRtĄũA2B2C2ĢŪēĒžÆËãRtĄũA1B1C1ÔÚÉÏĘöÐýŨŠđýģĖÖÐC1ËųūđýĩÄ·ģĖĢŪ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
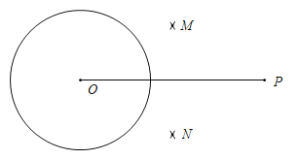
ĄūĖâÄŋĄŋÏÂÃæĘĮÐĄķŦÉčžÆĩÄĄ°đýÔēÍâŌŧĩãŨũÕâļöÔēĩÄÁ―ĖõĮÐÏߥąĩÄģßđæŨũÍžđýģĖĢŪ
ŌŅÖŠĢšĄŅOž°ĄŅOÍâŌŧĩãPĢŪ
ĮóŨũĢšÖąÏßPAšÍÖąÏßPBĢŽĘđPAĮÐĄŅOÓÚĩãAĢŽPBĮÐĄŅOÓÚĩãBĢŪ
Ũũ·ĻĢšČįÍžĢŽ
ĒŲÁŽ―ÓOPĢŽ·ÖąðŌÔĩãOšÍĩãPΊÔēÐÄĢŽīóÓÚ![]() OPĩÄÍŽŅųģĪΊ°ëūķŨũŧĄĢŽÁ―ŧĄ·Öąð―ŧÓÚĩãMĢŽNĢŧ
OPĩÄÍŽŅųģĪΊ°ëūķŨũŧĄĢŽÁ―ŧĄ·Öąð―ŧÓÚĩãMĢŽNĢŧ
ĒÚÁŽ―ÓMNĢŽ―ŧOPÓÚĩãQĢŽÔŲŌÔĩãQΊÔēÐÄĢŽOQĩÄģĪΊ°ëūķŨũŧĄĢŽ―ŧĄŅOÓÚĩãAšÍĩãBĢŧ
ĒÛŨũÖąÏßPAšÍÖąÏßPB.
ËųŌÔÖąÏßPAšÍPBūÍĘĮËųĮóŨũĩÄÖąÏß.
ļųūÝÐĄķŦÉčžÆĩÄģßđæŨũÍžđýģĖĢŽ
ĢĻ1ĢĐĘđÓÃÖąģßšÍÔēđæĢŽēđČŦÍžÐÎĢŧĢĻąĢÁôŨũÍžšÛžĢĢĐ
ĢĻ2ĢĐÍęģÉÏÂÃæĩÄÖĪÃũ.
ÖĪÃũĢšĄßOPĘĮĄŅQĩÄÖąūķĢŽ
Ąā ĄÏOAPĢ―ĄÏOBPĢ―________ĄãĢĻ ĢĐĢĻĖîÍÆĀíĩÄŌĀūÝĢĐĢŪ
ĄāPAĄÍOAĢŽPBĄÍOBĢŪ
ĄßOAĢŽOBΊĄŅOĩÄ°ëūķĢŽ
ĄāPAĢŽPBĘĮĄŅOĩÄĮÐÏßĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÅŨÎïÏß![]() ĩÄēŋ·ÖÍžÏóČįÍžËųĘūĢŽÓëxÖáĩÄŌŧļö―ŧĩãŨøąęΊ
ĩÄēŋ·ÖÍžÏóČįÍžËųĘūĢŽÓëxÖáĩÄŌŧļö―ŧĩãŨøąęΊ![]() ĢŽÅŨÎïÏßĩÄķÔģÆÖáĘĮ
ĢŽÅŨÎïÏßĩÄķÔģÆÖáĘĮ![]() ÏÂÁÐ―áÂÛÖÐĢš
ÏÂÁÐ―áÂÛÖÐĢš
![]() Ģŧ
Ģŧ![]() Ģŧ
Ģŧ![]() ·―ģĖ
·―ģĖ![]() ÓÐÁ―ļöēŧÏāĩČĩÄĘĩĘýļųĢŧ
ÓÐÁ―ļöēŧÏāĩČĩÄĘĩĘýļųĢŧ![]() ÅŨÎïÏßÓëxÖáĩÄÁíŌŧļö―ŧĩãŨøąęΊ
ÅŨÎïÏßÓëxÖáĩÄÁíŌŧļö―ŧĩãŨøąęΊ![]() Ģŧ
Ģŧ![]() Čôĩã
Čôĩã![]() ÔÚļÃÅŨÎïÏßÉÏĢŽÔō
ÔÚļÃÅŨÎïÏßÉÏĢŽÔō![]() ĢŪ
ĢŪ
ÆäÖÐÕýČ·ĩÄÓÐ![]() ĄĄĄĄ
ĄĄĄĄ![]()

A. 5ļö B. 4ļö C. 3ļö D. 2ļö
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋΊÏėÓĶūĢÖÝĘÐĄ°īī―ĻČŦđúÎÄÃũģĮĘÐĄąšÅÕŲĢŽÄģĩĨÎŧēŧķÏÃĀŧŊŧ·ūģĢŽÄâÔÚŌŧŋéūØÐÎŋÕĩØÉÏÐÞ―ĻÂĖÉŦÖēÎïÔ°ĢŽÆäÖÐŌŧąßŋŋĮ―ĢŽŋÉĀûÓÃĩÄĮ―ģĪēŧģŽđý18mĢŽÁíÍâČýąßÓÉ36mģĪĩÄÕĪĀļΧģÉĢŪÉčūØÐÎABCDŋÕĩØÖÐĢŽīđÖąÓÚĮ―ĩÄąßAB=xmĢŽÃæŧýΊym2ĢĻČįÍžĢĐĢŪ
ĢĻ1ĢĐĮóyÓëxÖŪžäĩÄšŊĘýđØÏĩĘ―ĢŽēĒÐīģöŨÔąäÁŋxĩÄČĄÖĩ·ķΧĢŧ
ĢĻ2ĢĐČôūØÐÎŋÕĩØĩÄÃæŧýΊ160m2ĢŽĮóxĩÄÖĩĢŧ
ĢĻ3ĢĐČôļÃĩĨÎŧÓÃ8600ÔŠđšÂōÁËžŨĄĒŌŌĄĒąûČýÖÖÂĖÉŦÖēÎïđē400ŋÃĢĻÃŋÖÖÖēÎïĩÄĩĨžÛšÍÃŋŋÃÔÔÖÖĩÄšÏĀíÓÃĩØÃæŧýČįÏÂąíĢĐĢŪÎĘąûÖÖÖēÎïŨîķāŋÉŌÔđšÂōķāÉŲŋÃĢŋīËĘąĢŽÕâÅúÖēÎïŋÉŌÔČŦēŋÔÔÖÖĩ―ÕâŋéŋÕĩØÉÏÂðĢŋĮëËĩÃũĀíÓÉĢŪ
žŨ | ŌŌ | ąû | |
ĩĨžÛĢĻÔŠ/ŋÃĢĐ | 14 | 16 | 28 |
šÏĀíÓÃĩØĢĻm2/ŋÃĢĐ | 0.4 | 1 | 0.4 |

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽĄũABCÄÚ―ÓÓÚĄŅOĢŽĄÏCBG=ĄÏAĢŽCDΊֹūķĢŽOCÓëABÏā―ŧÓÚĩãEĢŽđýĩãEŨũEFĄÍBCĢŽīđŨãΊFĢŽŅÓģĪCD―ŧGBĩÄŅÓģĪÏßÓÚĩãPĢŽÁŽ―ÓBDĢŪ
ĢĻ1ĢĐĮóÖĪĢšPGÓëĄŅOÏāĮÐĢŧ
ĢĻ2ĢĐČô![]() =
=![]() ĢŽĮó
ĢŽĮó![]() ĩÄÖĩĢŧ
ĩÄÖĩĢŧ
ĢĻ3ĢĐÔÚĢĻ2ĢĐĩÄĖõžþÏÂĢŽČôĄŅOĩÄ°ëūķΊ8ĢŽPD=ODĢŽĮóOEĩÄģĪĢŪ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
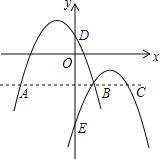
ĄūĖâÄŋĄŋČįÍžĢŽÅŨÎïÏßl1Ģšy1Ģ―a(x+1)2+2Óël2Ģšy2Ģ―Đ(xĐ2)2Đ1―ŧÓÚĩãB(1ĢŽĐ2)ĢŽĮŌ·ÖąðÓëyÖá―ŧÓÚĩãDĄĒEĢŪđýĩãBŨũxÖáĩÄÆ―ÐÐÏßĢŽ―ŧÅŨÎïÏßÓÚĩãAĄĒCĢŽÔōŌÔÏÂ―áÂÛĢš
ĒŲÎÞÂÛxČĄšÎÖĩĢŽy2ŨÜĘĮļšĘýĢŧ
ĒÚl2ŋÉÓÉl1ÏōÓŌÆ―ŌÆ3ļöĩĨÎŧĢŽÔŲÏōÏÂÆ―ŌÆ3ļöĩĨÎŧĩÃĩ―Ģŧ
ĒÛĩąĐ3ĢžxĢž1ĘąĢŽËæŨÅxĩÄÔöīóĢŽy1Đy2ĩÄÖĩÏČÔöīóšóžõÐĄĢŧ
ĒÜËÄąßÐÎAECDΊÕý·―ÐÎĢŪ
ÆäÖÐÕýČ·ĩÄĘĮ(ĄĄĄĄ)
A.1ļöB.2ļöC.3ļöD.4ļö
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
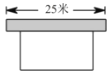
ĄūĖâÄŋĄŋČįÍžĢŽŌŠ―ĻŌŧļöģĪ·―ÐÎŅøžĶģĄĢŽŅøžĶģĄĩÄŌŧąßŋŋĮ―ĢĻĮ―ģĪ25ÃŨĢĐĢŽÁíČýąßÓÃÖņĀé°ĘΧģÉĢŽÖņĀé°ĘĩÄģĪΊ40ÃŨĢŽČôŌŠÎ§ģÉĩÄŅøžĶģĄĩÄÃæŧýΊ180Æ―·―ÃŨĢŽĮóŅøžĶģĄĩÄģĪĄĒŋíļũΊķāÉŲÃŨĢŽÉčÓëĮ―Æ―ÐÐĩÄŌŧąßģĪΊ![]() ÃŨĢŪ
ÃŨĢŪ
ĢĻ1ĢĐĖîŋÕĢšĢĻÓÚŽ![]() ĩÄīúĘýĘ―ąíĘūĢĐÁíŌŧąßģĪΊ ÃŨĢŧ
ĩÄīúĘýĘ―ąíĘūĢĐÁíŌŧąßģĪΊ ÃŨĢŧ
ĢĻ2ĢĐÁÐģö·―ģĖĢŽēĒĮóģöÎĘĖâĩÄ―âĢŪ
ēéŋīīð°ļšÍ―âÎö>>
đúžĘŅ§ÐĢÓÅŅĄ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com