Question

【题目】如图所示，在ABCD中，对角线AC与BD相交于点O，过点O作一条直线分别交AB，CD于点E，F．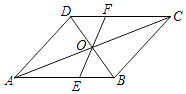
（1）求证：OE=OF；
（2）若AB=6，BC=5，OE=2，求四边形BCFE的周长．

Answer 1

【答案】
（1）证明：在□ABCD中，

∵AC与BD相交于点O，

∴OA=OC，AB∥CD，

∴∠OAE=∠OCF，在△OAE和△OCF中， ，

∴△OAE≌△OCF（ASA），

∴OE=OF．

（2）解：∵△OAE≌△OCF，

∴DF=AE，

∴BE+CF=AB=6，

又∵EF=2OE=4，

∴四边形BCFE的周长=BE+BE+CF+EF=6+4+5=15

【解析】（1）由四边形ABCD是平行四边形，可得OA=OC，AB∥CD，则可证得△AOE≌△COF（ASA），继而证得OE=OF；（2）由△AOE≌△COF（ASA），可得EF=2OE=4，BE+CF=AB=6，继而求得答案．
【考点精析】认真审题，首先需要了解平行四边形的性质(平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分)．