
【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

【答案】(1)详见解析;(2)详见解析;(3)1.
【解析】
(1)由于AB=AC,AD=AE,所以只需证∠BAD=∠CAE即可得结论;
(2)证明∠ACE和∠ECF都等于60°即可;
(3)将四边形ADCE的周长用AD表示,AD最小时就是四边形ADCE的周长最小,根据垂线段最短原理,当AD⊥BC时,AD最小,此时BD就是BC的一半.
(1)证明:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵∠DAE=60°,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,
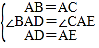 ,
,
∴△ABD≌△ACE.
(2)证明:∵△ABC是等边三角形,
∴∠B=∠BCA=60°,
∵△ABD≌△ACE,
∴∠ACE=∠B=60°,
∵△ABD≌△ACE,
∴∠ACE=∠B=60°,
∴∠ECF=180﹣∠ACE﹣∠BCA=60°,
∴∠ACE=∠ECF,
∴CE平分∠ACF.
(3)解:∵△ABD≌△ACE,
∴CE=BD,
∵△ABC是等边三角形,
∴AB=BC=AC=2,
∴四边形ADCE的周长=CE+DC+AD+AE=BD+DC+2AD=2+2AD,
根据垂线段最短,当AD⊥BC时,AD值最小,四边形ADCE的周长取最小值,
∵AB=AC,
∴BD=![]() BC=
BC=![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,即确定一个月销售目标,根据目标完成的情况对营业员进行适当的奖惩.为了确定一个适当的目标,商场统计了每个营业员在某月的销售额,统计图如下:
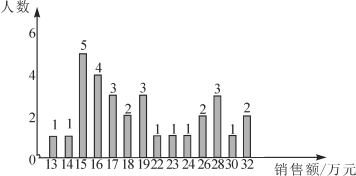
请你结合统计图和平均数、众数和中位数解答下列问题:(结果保留整数)
(1)月销售额在哪个值的人最多?月销售额处于中间的是多少?月平均销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4
∵(y+2)2≥0
∴(y+2)2+4≥4
∴y2+4y+8的最小值是4.
(1)求代数式m2+m+4的最小值;
(2)求代数式4﹣x2+2x的最大值;
(3)某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
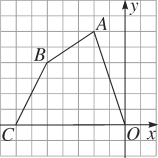
【题目】如图,有一块不规则的四边形地皮ABCO,各个顶点的坐标分别为A(-2,6),B(-5,4),C(-7,0),O(0,0)(图上一个单位长度表示10米),现在想对这块地皮进行规划,需要确定它的面积.
(1)求这个四边形的面积;
(2)如果把四边形ABCD的各个顶点的纵坐标保持不变,横坐标加2,所得到的四边形面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方法回顾:在进行数值估算时,我们常根据所求数值的条件确定它的大致范围,然后通过逐步缩小数值存在范围的方法,最终求得较为准确的数值.
如我们在探究面积为2的正方形的边长a的值时,有如下探究过程:
1<a<2 | 1<s<4 |
1.4<a<1.5 | 1.96<s<2.25 |
1.41<a<1.42 | 1.9881<s<2.0164 |
1.414<a<1.415 | 1.999396<s<2.002225 |
我们也可以借助数轴直观地看出“逐步缩小数值的存在范图”的过程,

这种方法在我们的解决向题的过程中经常会用到
问题提出:a是小于100的正整数,已知它的立方,不借助计算器,如何确定a呢?
问题探究:我们不妨由简单到复杂,从一位整数的立方开始硏究
步骤一、若13<a3<103,则1<a<10.即已知一个一位整数的立方为a3,怎样确定a?
易得:13=1,23=8,33=27,43=64,53=125,63=216,73=343:83=512,93=729,可以通过从1到9的九个整数的立方值确定这个数.观察这九个立方值我们还能发现,他们的个位数字各不相同.
步骤二、若103<a3<1003.则10<a<100,即已知一个两位数的立方为a3,怎样确定a?我们不妨举几个特例,以便寻找解决问题的方法.
特例1.如果一个两位整数a的立方是5832,怎样确定a?
因为103<5832<1003,所以10<a<100,a是一个两位数.
又因为103<5832<203,所以我们可以确定5832的十位数字是 ;再根据步骤一我们就能得出它的个位数是 ;从而确定这个两位数是 .
特例2.如果x是一个两位整数,且x3=614125,请你仿照上面的过程说明你确定这个两位整数的方法.
拓展应用:一颗近似球形的小行星的体积的为2624000πm3,请你根据以上方法求出这个小行星的半径.(球的体积公式v=![]() πR3)
πR3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC,BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( )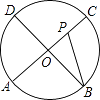
A.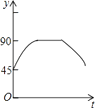
B.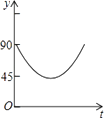
C.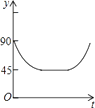
D.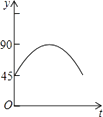
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,两个函数y=x,y=﹣![]() x+6的图象交于点A.动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S.
x+6的图象交于点A.动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S.
(1)求点A的坐标.
(2)试求出点P在线段OA上运动时,S与运动时间t(秒)的关系式.
(3)在(2)的条件下,S是否有最大值若有,求出t为何值时,S有最大值,并求出最大值;若没有,请说明理由.
(4)若点P经过点A后继续按原方向、原速度运动,当正方形PQMN与△OAB重叠部分面积最大时,运动时间t满足的条件是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
(1)请用两种不同方法,求图2中阴影部分的面积(不用化简)
方法1:____________________
方法2:____________________
(2)观察图2,写出![]() ,
,![]() ,
,![]() 之间的等量关系,并验证;
之间的等量关系,并验证;

(3)根据(2)题中的等量关系,解决如下问题:
①若![]() ,
,![]() ,求
,求![]() 的值;
的值;
②若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F. 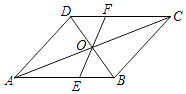
(1)求证:OE=OF;
(2)若AB=6,BC=5,OE=2,求四边形BCFE的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com