
【题目】如图,有一块不规则的四边形地皮ABCO,各个顶点的坐标分别为A(-2,6),B(-5,4),C(-7,0),O(0,0)(图上一个单位长度表示10米),现在想对这块地皮进行规划,需要确定它的面积.
(1)求这个四边形的面积;
(2)如果把四边形ABCD的各个顶点的纵坐标保持不变,横坐标加2,所得到的四边形面积是多少?
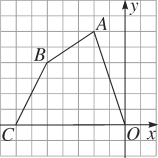
【答案】(1) 2500平方米;(2)所得到的四边形的面积与原四边形的面积相等,为2500平方米.
【解析】
(1)过点A作AG⊥x轴于点G,过点B作BF⊥x轴于点F,把四边形ABCO的面积分成两个三角形的面积与梯形的面积的和,然后列式求解即可;
(2)横坐标增加2,纵坐标不变,就是把四边形ABCO向右平移2个单位,根据平移的性质,四边形的面积不变.
(1)过B作BF⊥x轴于F,过A作AG⊥x轴于G,如图所示.
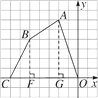
∴S四边形ABCO=S三角形BCF+S梯形ABFG+S三角形AGO
=[![]() ]
]
×102=2500(平方米).
(2)把四边形ABCO的各个顶点的纵坐标保持不变,横坐标加2,即将这个四边形向右平移2个单位长度,
故所得到的四边形的面积与原四边形的面积相等,为2500平方米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1所示,等边△ABC中,AD是BC边上的中线,根据等腰三角形的“三线合一”特性,AD平分∠BAC,且AD⊥BC,则有∠BAD=30°,BD=CD=![]() AB.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
AB.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
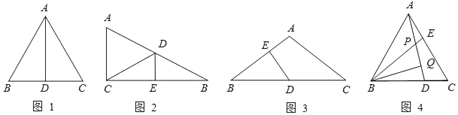
请根据从上面材料中所得到的信息解答下列问题:
(1)如图2所示,在△ABC中,∠ACB=90°,BC的垂直平分线交AB于点D,垂足为E,当BD=5cm,∠B=30°时,求△ACD的周长.
(2)如图3所示,在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足为E,求BE:EA的值.
(3)如图4所示,在等边△ABC中,D、E分别是BC、AC上的点,且AE=DC,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)若∠AOC=30°时,则∠DOE的度数为_____;
(2)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,其它条件不变,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
(3)将图①中的∠COD绕顶点O顺时针旋转至图③的位置,其他条件不变.直接写出∠AOC和∠DOE的度数之间的关系:_____.
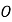
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
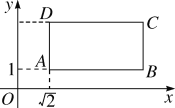
【题目】如图,长方形ABCD在坐标平面内,点A的坐标是A(![]() ,1),且边AB,CD与x轴平行,边AD,BC与y轴平行,AB=4,AD=2.
,1),且边AB,CD与x轴平行,边AD,BC与y轴平行,AB=4,AD=2.
(1)求B,C,D三点的坐标;
(2)怎样平移,才能使A点与原点O重合?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)材料1:一般地,n个相同因数a相乘:![]() 记为
记为 ![]() 如
如![]() ,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么,log39=________,
,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么,log39=________,![]() =________;
=________;
(2)材料2:新规定一种运算法则:自然数1到n的连乘积用n!表示,例如:1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…在这种规定下,请你解决下列问题:
①算5!=________;
②已知x为整数,求出满足该等式的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com