
【题目】如图1所示,等边△ABC中,AD是BC边上的中线,根据等腰三角形的“三线合一”特性,AD平分∠BAC,且AD⊥BC,则有∠BAD=30°,BD=CD=![]() AB.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
AB.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
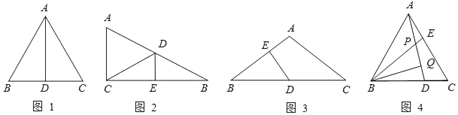
请根据从上面材料中所得到的信息解答下列问题:
(1)如图2所示,在△ABC中,∠ACB=90°,BC的垂直平分线交AB于点D,垂足为E,当BD=5cm,∠B=30°时,求△ACD的周长.
(2)如图3所示,在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足为E,求BE:EA的值.
(3)如图4所示,在等边△ABC中,D、E分别是BC、AC上的点,且AE=DC,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求PQ的长.
【答案】(1)15cm;(2)3:1;(3)PQ=1.
【解析】
(1)根据线段垂直平分线的性质知CD=BD,得出△ACD的周长=AC+AB;
(2)连接AD.利用等腰三角形的性质、垂直的定义推知∠B=∠ADE=30°,然后由”30度角所对的直角边是斜边的一半“分别求得BE、AE的值,即可得出结果;
(3)根据全等三角形的判定定理SAS证明△BAE≌△ACD,根据全等三角形的对应角相等,以及三角形外角的性质,可以得到∠PBQ=30°,根据直角三角形的性质得出PQ=1,再由勾股定理求出BQ即可.
解:(1)∵DE是线段BC的垂直平分线,∠ACB=90°,
∴CD=BD,AD=BD.
又∵在△ABC中,∠ACB=90°,∠B=30°,
∴![]()
∴△ACD的周长=AC+AB=3BD=15cm.
故答案为:15cm;
(2)如图,连接AD,
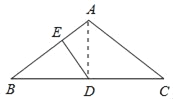
∵在△ABC中,AB=AC,∠A=120°,D是BC的中点,
∴∠BAD=60°.
又∵DE⊥AB,
∴∠B=∠ADE=30°,
∴![]()
∴![]()
又∵![]()
∴BE:AE=3:1.
故答案为:3:1.
(3)∵△ABC为等边三角形.
∴AB=AC,∠BAC=∠ACB=60°,
在△BAE和△ACD中,
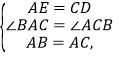
∴△BAE≌△ACD(SAS),
∴∠ABE=∠CAD.
∵∠BPQ为△ABP外角,
∴∠BPQ=∠ABE+∠BAD.
∴∠BPQ=∠CAD+∠BAD=∠BAC=60°
∵BQ⊥AD,
∴∠PBQ=30°,
∴BP=2PQ=2,
∴PQ=1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】读句画图:如图,直线CD与直线AB相交于C,
根据下列语句画图:
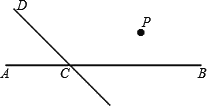
(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家距离学校8千米,一天早晨小亮骑车上学,途中恰好遇到交警叔叔在十字路口带领小朋友过马路,小亮停下车协助交警叔叔,几分钟后,为了不迟到,他加快了骑车到校的速度.到校后,小亮根据这段经历画出了过程图象如图.该图象描绘了小亮骑行的路程![]() (千米)与他所用的时间
(千米)与他所用的时间![]() (分钟)之间的关系,请根据图象,解答下列问题:
(分钟)之间的关系,请根据图象,解答下列问题:
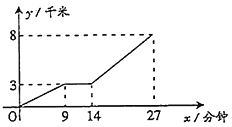
(1)小亮骑车行驶了多少千米时,协助交警叔叔?协助交警叔叔用了几分钟?
(2)小亮从家出发到学校共用了多少时间?
(3)如果没有协助交警叔叔,仍保持出发时的速度行驶,那么他比实际情况早到或晚到学校多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 与
与![]() 是否平行?为什么?
是否平行?为什么?
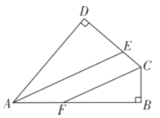
对于上述问题,小红给出了解答过程,请你在以下解答过程的括号内填上适当的内容
解:![]()
理由如下:
![]() ,
,
![]() .
.
∵四边形![]() 的内角和为360°,
的内角和为360°,
∴( ① )+( ② )=180°,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
![]() .
.
![]() .
.
又![]() , ( ③ )
, ( ③ )
![]() ,
,
![]() . ( ④ )
. ( ④ )
![]() .( ⑤ )
.( ⑤ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】微信运动和腾讯公益推出了一个爱心公益活动:一天中走路步数达到10000步及以上可通过微信运动和腾讯基金会向公益活动捐款,如果步数在10000步及以上,每步可捐0.0002元;若步数在10000步以下,则不能参与捐款.
(1)老赵某天的步数为13000步,则他当日可捐多少钱?
(2)已知甲、乙、丙三人某天通过步数共捐了8.4元,且甲的步数=乙的步数=丙步数的3倍,则丙走了多少步?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,即确定一个月销售目标,根据目标完成的情况对营业员进行适当的奖惩.为了确定一个适当的目标,商场统计了每个营业员在某月的销售额,统计图如下:
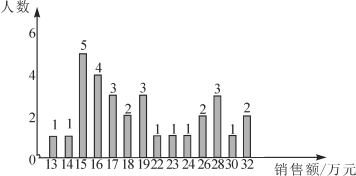
请你结合统计图和平均数、众数和中位数解答下列问题:(结果保留整数)
(1)月销售额在哪个值的人最多?月销售额处于中间的是多少?月平均销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线上一点![]() 为端点作射线
为端点作射线![]() ,使
,使![]() .将一个直角三角板
.将一个直角三角板![]() (其中
(其中![]() )的直角顶点放在点
)的直角顶点放在点![]() 处.
处.
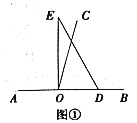
(1)如图①,若直角三角板![]() 的一边
的一边![]() 放在射线
放在射线![]() 上,则
上,则![]() ____
____![]() ;
;
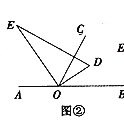
(2)如图②,将直角三角板![]() 绕点
绕点![]() 逆时针转动到某个位置,若
逆时针转动到某个位置,若![]() 恰好平分
恰好平分![]() ,则
,则![]() 所在的射线是否为
所在的射线是否为![]() 的平分线?请说明理由;
的平分线?请说明理由;
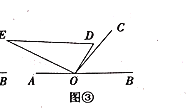
(3)如图③,将含![]() 角的直角三角板
角的直角三角板![]() 从图①的位置开始绕点
从图①的位置开始绕点![]() 以每秒
以每秒![]() 的速度逆时针旋转,设旋转角为
的速度逆时针旋转,设旋转角为![]() ,旋转的时间为
,旋转的时间为![]() 秒,在旋转过程中是否存在三角板的一条边与
秒,在旋转过程中是否存在三角板的一条边与![]() 垂直?若存在,请直接写出此时
垂直?若存在,请直接写出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
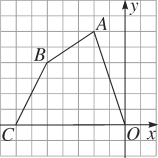
【题目】如图,有一块不规则的四边形地皮ABCO,各个顶点的坐标分别为A(-2,6),B(-5,4),C(-7,0),O(0,0)(图上一个单位长度表示10米),现在想对这块地皮进行规划,需要确定它的面积.
(1)求这个四边形的面积;
(2)如果把四边形ABCD的各个顶点的纵坐标保持不变,横坐标加2,所得到的四边形面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com