
【题目】小亮家距离学校8千米,一天早晨小亮骑车上学,途中恰好遇到交警叔叔在十字路口带领小朋友过马路,小亮停下车协助交警叔叔,几分钟后,为了不迟到,他加快了骑车到校的速度.到校后,小亮根据这段经历画出了过程图象如图.该图象描绘了小亮骑行的路程![]() (千米)与他所用的时间
(千米)与他所用的时间![]() (分钟)之间的关系,请根据图象,解答下列问题:
(分钟)之间的关系,请根据图象,解答下列问题:
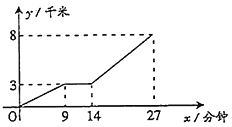
(1)小亮骑车行驶了多少千米时,协助交警叔叔?协助交警叔叔用了几分钟?
(2)小亮从家出发到学校共用了多少时间?
(3)如果没有协助交警叔叔,仍保持出发时的速度行驶,那么他比实际情况早到或晚到学校多少分钟?
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:
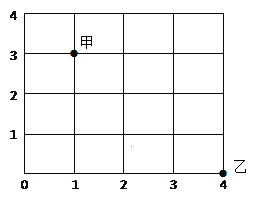
【题目】如图,甲处表示两条路的交叉口,乙处也是两条路的交叉口,如果用(1,3)表示甲处的位置,那么“(1,3)→(2,3)→(3,3)→(4,3)→(4,2)→(4,1)→(4,0)”表示甲处到乙处的一种路线,若图中一个单位长度表示5Km,请你用上述表示法写出甲处到乙处的另两种走法,最短距离是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2+(3m+1)x+3=0. 
(1)求证:该方程有两个实数根;
(2)如果抛物线y=mx2+(3m+1)x+3与x轴交于A、B两个整数点(点A在点B左侧),且m为正整数,求此抛物线的表达式;
(3)在(2)的条件下,抛物线y=mx2+(3m+1)x+3与y轴交于点C,点B关于y轴的对称点为D,设此抛物线在﹣3≤x≤﹣ ![]() 之间的部分为图象G,如果图象G向右平移n(n>0)个单位长度后与直线CD有公共点,求n的取值范围.
之间的部分为图象G,如果图象G向右平移n(n>0)个单位长度后与直线CD有公共点,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=8,延长线段AB至C,使得BC=![]() AB,延长线段BA至D,使得AD=
AB,延长线段BA至D,使得AD=![]() AB,则下列判断正确的是 ( )
AB,则下列判断正确的是 ( )
A. BC=![]() AD B. BD=3BC C. BD=4AD D. AC=6AD
AD B. BD=3BC C. BD=4AD D. AC=6AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆O的内接四边形ABCD中,BC=DC,∠BOC=130°,则∠BAD的度数是( ).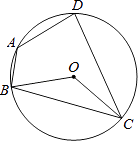
A.120°
B.130°
C.140°
D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“表1”为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分) | 70 | 80 | 90 |
男生(人) | 5 | 10 | 7 |
女生(人) | 4 | 13 | 4 |
A.男生的平均成绩大于女生的平均成绩
B.男生的平均成绩小于女生的平均成绩
C.男生成绩的中位数大于女生成绩的中位数
D.男生成绩的中位数小于女生成绩的中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,等边△ABC中,AD是BC边上的中线,根据等腰三角形的“三线合一”特性,AD平分∠BAC,且AD⊥BC,则有∠BAD=30°,BD=CD=![]() AB.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
AB.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
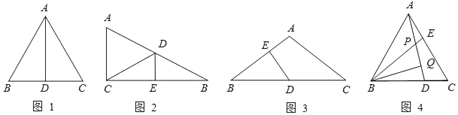
请根据从上面材料中所得到的信息解答下列问题:
(1)如图2所示,在△ABC中,∠ACB=90°,BC的垂直平分线交AB于点D,垂足为E,当BD=5cm,∠B=30°时,求△ACD的周长.
(2)如图3所示,在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足为E,求BE:EA的值.
(3)如图4所示,在等边△ABC中,D、E分别是BC、AC上的点,且AE=DC,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD(图1)按如下步骤操作:
(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);
(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);
(3)将纸片收展平,那么∠AFE的度数为( )

A. 60° B. 67.5° C. 72° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com