
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,即确定一个月销售目标,根据目标完成的情况对营业员进行适当的奖惩.为了确定一个适当的目标,商场统计了每个营业员在某月的销售额,统计图如下:
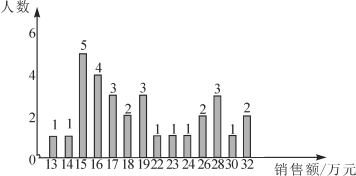
请你结合统计图和平均数、众数和中位数解答下列问题:(结果保留整数)
(1)月销售额在哪个值的人最多?月销售额处于中间的是多少?月平均销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?请说明理由.
【答案】(1) 月销售额在15万元的人最多;月销售额处于中间的是18万元;月平均销售额是20万元;(2)月销售额定为每月20万元是一个较高的目标.理由见解析.
【解析】
众数是出现次数最多的数,平均数是所有数据之和除以数据的个数,中位数是从小到大排列之后处于中间位置的一个数或者处于中间位置的两个数的平均数,运用众数,中位数和平均数的定义解答.
(1)因为众数为15万元,所以月销售额在15万元的人最多;总人数为30人,处于中间位置的是第15和16个人,他们的销售额均为18万元,即中位数是18万元,所以月销售额处于中间的是18万元;月平均销售额是(13+14+15×5+16×4+17×3+18×2+19×3+22+23+24+26×2+28×3+30+32×2)÷30≈20(万元)
(2)因为平均数、中位数和众数分别为20万元、18万元和15万元,而平均数最大,所以月销售额定为每月20万元是一个较高的目标.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】A、B两市相距150千米,分别从A、B处测得国家级风景区中心C处的方向角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.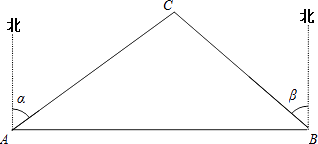
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆O的内接四边形ABCD中,BC=DC,∠BOC=130°,则∠BAD的度数是( ).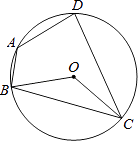
A.120°
B.130°
C.140°
D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,等边△ABC中,AD是BC边上的中线,根据等腰三角形的“三线合一”特性,AD平分∠BAC,且AD⊥BC,则有∠BAD=30°,BD=CD=![]() AB.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
AB.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
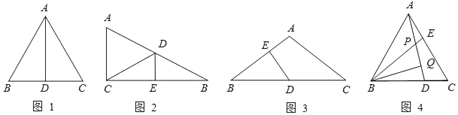
请根据从上面材料中所得到的信息解答下列问题:
(1)如图2所示,在△ABC中,∠ACB=90°,BC的垂直平分线交AB于点D,垂足为E,当BD=5cm,∠B=30°时,求△ACD的周长.
(2)如图3所示,在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足为E,求BE:EA的值.
(3)如图4所示,在等边△ABC中,D、E分别是BC、AC上的点,且AE=DC,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.
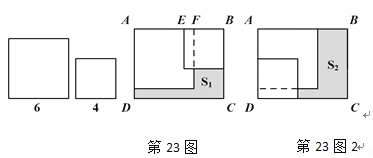
(1)在图1中,EF= ,BF= ;(用含m的式子表示)
(2)请用含m、n的式子表示图1,图2中的s1,s2,若m-n=2,请问S2-S1的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD(图1)按如下步骤操作:
(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);
(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);
(3)将纸片收展平,那么∠AFE的度数为( )

A. 60° B. 67.5° C. 72° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形纸片ABCD的边长为2,∠ABC=60°,将菱形ABCD沿EF,GH折叠,使得点B,D两点重合于对角线BD上一点P(如图2),则六边形AEFCHG面积的最大值是( ) 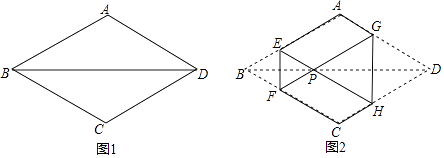
A.![]()
B.![]()
C.2﹣ ![]()
D.1+ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)若∠AOC=30°时,则∠DOE的度数为_____;
(2)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,其它条件不变,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
(3)将图①中的∠COD绕顶点O顺时针旋转至图③的位置,其他条件不变.直接写出∠AOC和∠DOE的度数之间的关系:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com