
ЁОЬтФПЁПвджБЯпЩЯвЛЕу![]() ЮЊЖЫЕузїЩфЯп
ЮЊЖЫЕузїЩфЯп![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЎНЋвЛИіжБНЧШ§НЧАх
ЃЎНЋвЛИіжБНЧШ§НЧАх![]() ЃЈЦфжа
ЃЈЦфжа![]() ЃЉЕФжБНЧЖЅЕуЗХдкЕу
ЃЉЕФжБНЧЖЅЕуЗХдкЕу![]() ДІЃЎ
ДІЃЎ
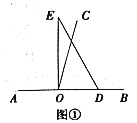
ЃЈ1ЃЉШчЭМЂйЃЌШєжБНЧШ§НЧАх![]() ЕФвЛБп
ЕФвЛБп![]() ЗХдкЩфЯп
ЗХдкЩфЯп![]() ЩЯЃЌдђ
ЩЯЃЌдђ![]() ____
____![]() ЃЛ
ЃЛ
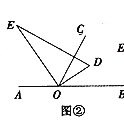
ЃЈ2ЃЉШчЭМЂкЃЌНЋжБНЧШ§НЧАх![]() ШЦЕу
ШЦЕу![]() ФцЪБеызЊЖЏЕНФГИіЮЛжУЃЌШє
ФцЪБеызЊЖЏЕНФГИіЮЛжУЃЌШє![]() ЧЁКУЦНЗж
ЧЁКУЦНЗж![]() ЃЌдђ
ЃЌдђ![]() ЫљдкЕФЩфЯпЪЧЗёЮЊ
ЫљдкЕФЩфЯпЪЧЗёЮЊ![]() ЕФЦНЗжЯпЃПЧыЫЕУїРэгЩЃЛ
ЕФЦНЗжЯпЃПЧыЫЕУїРэгЩЃЛ
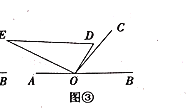
ЃЈ3ЃЉШчЭМЂлЃЌНЋКЌ![]() НЧЕФжБНЧШ§НЧАх
НЧЕФжБНЧШ§НЧАх![]() ДгЭМЂйЕФЮЛжУПЊЪМШЦЕу
ДгЭМЂйЕФЮЛжУПЊЪМШЦЕу![]() вдУПУы
вдУПУы![]() ЕФЫйЖШФцЪБеыа§зЊЃЌЩша§зЊНЧЮЊ
ЕФЫйЖШФцЪБеыа§зЊЃЌЩша§зЊНЧЮЊ![]() ЃЌа§зЊЕФЪБМфЮЊ
ЃЌа§зЊЕФЪБМфЮЊ![]() УыЃЌдка§зЊЙ§ГЬжаЪЧЗёДцдкШ§НЧАхЕФвЛЬѕБпгы
УыЃЌдка§зЊЙ§ГЬжаЪЧЗёДцдкШ§НЧАхЕФвЛЬѕБпгы![]() ДЙжБЃПШєДцдкЃЌЧыжБНгаДГіДЫЪБ
ДЙжБЃПШєДцдкЃЌЧыжБНгаДГіДЫЪБ![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ30ЃЛЃЈ2ЃЉЪЧЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉДцдкЃЌ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉДњШыЁЯBOE=ЁЯCOE+ЁЯCOBЧѓГіМДПЩЃЛ
ЃЈ2ЃЉгЩ![]() ЦНЗж
ЦНЗж![]() ЧѓГі
ЧѓГі![]() ЃЌИљОнНЧЕФКЭВюЧѓГі
ЃЌИљОнНЧЕФКЭВюЧѓГі![]() ЃЌ
ЃЌ![]() ЃЌДгЖјЭЦГіЁЯCOD=ЁЯDOBЃЌМДПЩЕУГіНсТлЃЛ
ЃЌДгЖјЭЦГіЁЯCOD=ЁЯDOBЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЗжDEЁЭOCгкЕуMЪБЃЌOEЁЭOCЪБЃЌODЁЭOCЪБЃЌШ§жжЧщПіЗжБ№СаЗНГЬЧѓНтЃЎ
НтЃКЃЈ1ЃЉЁпЁЯBOE=ЁЯCOE+ЁЯCOB=90ЁуЃЌ
гжЁпЁЯCOB=60ЁуЃЌ
ЁрЁЯCOE=30ЁуЃЌ
ЙЪД№АИЮЊЃК30ЃЛ
ЃЈ2ЃЉ![]() ЫљдкЕФЩфЯпЪЧ
ЫљдкЕФЩфЯпЪЧ![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп
РэгЩШчЯТЃК
![]()
![]()
![]() ЦНЗж
ЦНЗж![]()
![]()
![]()
![]()
![]()
![]() ЫљдкЕФЩфЯпЦНЗж
ЫљдкЕФЩфЯпЦНЗж![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЂйЕБDEЁЭOCгкЕуMЪБ
гЩЬтвтПЩжЊЃЌжБНЧШ§НЧАхжаЁЯD=60Ёу
ЁрДЫЪБЁЯCOD=30ЁуЃЌЁЯBOD=ЁЯBOC-ЁЯCOD=30Ёу
10t=30ЃЌНтЕУt=3ЃЛ
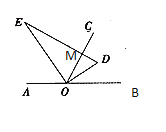
ЂкЕБOEЁЭOCЪБ
ДЫЪБЕуDдкOCЩЯЃЌЁЯBOC=60Ёу
10t=60ЃЌНтЕУt=6ЃЛ

ЂлЕБODЁЭOCЪБЃЌ
ДЫЪБЁЯBOD=60Ёу+90Ёу=150Ёу
10t=150ЃЌНтЕУt=15
злЩЯЫљЪіЃЌ![]() Лђ
Лђ![]() ЪБЃЌШ§НЧАхЕФвЛЬѕБпгы
ЪБЃЌШ§НЧАхЕФвЛЬѕБпгы![]() ДЙжБЃЎ
ДЙжБЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬmx2+ЃЈ3m+1ЃЉx+3=0ЃЎ 
ЃЈ1ЃЉЧѓжЄЃКИУЗНГЬгаСНИіЪЕЪ§ИљЃЛ
ЃЈ2ЃЉШчЙћХзЮяЯпy=mx2+ЃЈ3m+1ЃЉx+3гыxжсНЛгкAЁЂBСНИіећЪ§ЕуЃЈЕуAдкЕуBзѓВрЃЉЃЌЧвmЮЊе§ећЪ§ЃЌЧѓДЫХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌХзЮяЯпy=mx2+ЃЈ3m+1ЃЉx+3гыyжсНЛгкЕуCЃЌЕуBЙигкyжсЕФЖдГЦЕуЮЊDЃЌЩшДЫХзЮяЯпдкЉ3ЁмxЁмЉ ![]() жЎМфЕФВПЗжЮЊЭМЯѓGЃЌШчЙћЭМЯѓGЯђгвЦНвЦnЃЈnЃО0ЃЉИіЕЅЮЛГЄЖШКѓгыжБЯпCDгаЙЋЙВЕуЃЌЧѓnЕФШЁжЕЗЖЮЇЃЎ
жЎМфЕФВПЗжЮЊЭМЯѓGЃЌШчЙћЭМЯѓGЯђгвЦНвЦnЃЈnЃО0ЃЉИіЕЅЮЛГЄЖШКѓгыжБЯпCDгаЙЋЙВЕуЃЌЧѓnЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
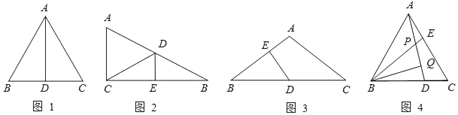
ЁОЬтФПЁПШчЭМ1ЫљЪОЃЌЕШБпЁїABCжаЃЌADЪЧBCБпЩЯЕФжаЯпЃЌИљОнЕШбќШ§НЧаЮЕФЁАШ§ЯпКЯвЛЁБЬиадЃЌADЦНЗжЁЯBACЃЌЧвADЁЭBCЃЌдђгаЁЯBADЃН30ЁуЃЌBDЃНCDЃН![]() ABЃЎгкЪЧПЩЕУГіНсТлЁАжБНЧШ§НЧаЮжаЃЌ30ЁуНЧЫљЖдЕФжБНЧБпЕШгкаББпЕФвЛАыЁБЃЎ
ABЃЎгкЪЧПЩЕУГіНсТлЁАжБНЧШ§НЧаЮжаЃЌ30ЁуНЧЫљЖдЕФжБНЧБпЕШгкаББпЕФвЛАыЁБЃЎ
ЧыИљОнДгЩЯУцВФСЯжаЫљЕУЕНЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉШчЭМ2ЫљЪОЃЌдкЁїABCжаЃЌЁЯACBЃН90ЁуЃЌBCЕФДЙжБЦНЗжЯпНЛABгкЕуDЃЌДЙзуЮЊEЃЌЕБBDЃН5cmЃЌЁЯBЃН30ЁуЪБЃЌЧѓЁїACDЕФжмГЄЃЎ
ЃЈ2ЃЉШчЭМ3ЫљЪОЃЌдкЁїABCжаЃЌABЃНACЃЌЁЯAЃН120ЁуЃЌDЪЧBCЕФжаЕуЃЌDEЁЭABЃЌДЙзуЮЊEЃЌЧѓBEЃКEAЕФжЕЃЎ
ЃЈ3ЃЉШчЭМ4ЫљЪОЃЌдкЕШБпЁїABCжаЃЌDЁЂEЗжБ№ЪЧBCЁЂACЩЯЕФЕуЃЌЧвAEЃНDCЃЌADЁЂBEНЛгкЕуPЃЌзїBQЁЭADгкQЃЌШєBPЃН2ЃЌЧѓPQЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋОиаЮжНЦЌABCDЃЈЭМ1ЃЉАДШчЯТВНжшВйзїЃК
ЃЈ1ЃЉвдЙ§ЕуAЕФжБЯпЮЊелКлелЕўжНЦЌЃЌЪЙЕуBЧЁКУТфдкADБпЩЯЃЌелКлгыBCБпНЛгкЕуEЃЈШчЭМ2ЃЉЃЛ
ЃЈ2ЃЉвдЙ§ЕуEЕФжБЯпЮЊелКлелЕўжНЦЌЃЌЪЙЕуAТфдкBCБпЩЯЃЌелКлEFНЛADБпгкЕуFЃЈШчЭМ3ЃЉЃЛ
ЃЈ3ЃЉНЋжНЦЌЪееЙЦНЃЌФЧУДЁЯAFEЕФЖШЪ§ЮЊЃЈЁЁЁЁЃЉ

A. 60Ёу B. 67.5Ёу C. 72Ёу D. 75Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌСтаЮжНЦЌABCDЕФБпГЄЮЊ2ЃЌЁЯABC=60ЁуЃЌНЋСтаЮABCDбиEFЃЌGHелЕўЃЌЪЙЕУЕуBЃЌDСНЕужиКЯгкЖдНЧЯпBDЩЯвЛЕуPЃЈШчЭМ2ЃЉЃЌдђСљБпаЮAEFCHGУцЛ§ЕФзюДѓжЕЪЧЃЈ ЃЉ 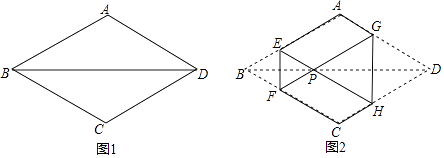
A.![]()
B.![]()
C.2Љ ![]()
D.1+ ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
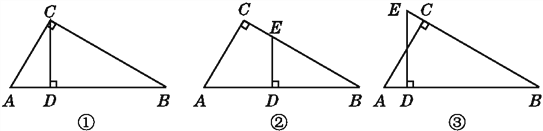
ЁОЬтФПЁП(1)ШчЭМЂй,CDЪЧжБНЧШ§НЧаЮABCаББпABЩЯЕФИп,ЭМжагагыЁЯAЯрЕШЕФНЧТ№?ЮЊЪВУД?
(2)ШчЭМЂк,АбЭМЂйжаЕФCDЦНвЦЕНEDДІ,ЭМжаЛЙгагыЁЯAЯрЕШЕФНЧТ№?ЮЊЪВУД?
(3)ШчЭМЂл,АбЭМЂйжаЕФCDЦНвЦЕНEDДІ,НЛBCЕФбгГЄЯпгкЕуE,ЭМжаЛЙгагыЁЯAЯрЕШЕФНЧТ№?ЮЊЪВУД?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
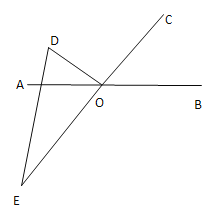
ЁОЬтФПЁПШчЭМЂйЃЌOЪЧжБЯпABЩЯЕФвЛЕуЃЌЁЯCODЪЧжБНЧЃЌOEЦНЗжЁЯBOCЃЎ
ЃЈ1ЃЉШєЁЯAOC=30ЁуЪБЃЌдђЁЯDOEЕФЖШЪ§ЮЊ_____ЃЛ
ЃЈ2ЃЉНЋЭМЂйжаЕФЁЯCODШЦЖЅЕуOЫГЪБеыа§зЊжСЭМЂкЕФЮЛжУЃЌЦфЫќЬѕМўВЛБфЃЌЬНОПЁЯAOCКЭЁЯDOEЕФЖШЪ§жЎМфЕФЙиЯЕЃЌаДГіФуЕФНсТлЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉНЋЭМЂйжаЕФЁЯCODШЦЖЅЕуOЫГЪБеыа§зЊжСЭМЂлЕФЮЛжУЃЌЦфЫћЬѕМўВЛБфЃЎжБНгаДГіЁЯAOCКЭЁЯDOEЕФЖШЪ§жЎМфЕФЙиЯЕЃК_____ЃЎ
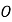
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌCЮЊЯпЖЮABЩЯвЛЕуЃЌЕуDЮЊBCЕФжаЕуЃЌЧвABЃН18cmЃЌACЃН4CDЃЎ
ЃЈ1ЃЉЭМжаЙВгаЁЁ ЁЁЬѕЯпЖЮЃЛ
ЃЈ2ЃЉЧѓACЕФГЄЃЛ
ЃЈ3ЃЉШєЕуEдкжБЯпABЩЯЃЌЧвEAЃН2cmЃЌЧѓBEЕФГЄЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌBDЪЧЖдНЧЯпЃЌЧвDBЁЭBCЃЌEЁЂFЗжБ№ЮЊБпABЁЂCDЕФжаЕуЃЎЧѓжЄЃКЫФБпаЮDEBFЪЧСтаЮЃЎ 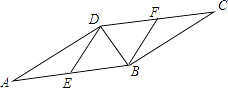
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com